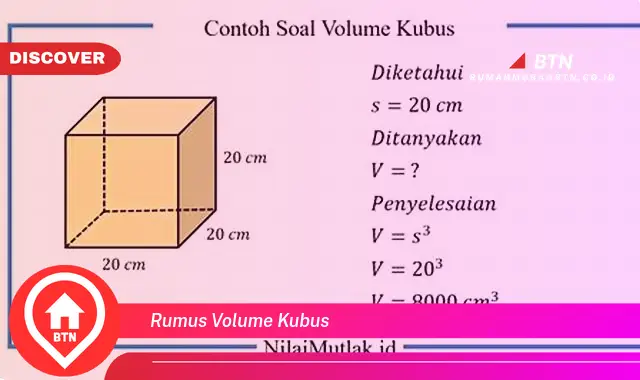
Rumus volume kubus adalah persamaan matematika yang digunakan untuk menghitung volume kubus, sebuah bangun ruang tiga dimensi dengan enam sisi berbentuk persegi. Rumus ini menyatakan bahwa volume kubus sama dengan panjang rusuk kubus pangkat tiga. Misalnya, jika panjang rusuk suatu kubus adalah 5 cm, maka volumenya adalah 5 cm x 5 cm x 5 cm = 125 cm3.
Rumus volume kubus sangat penting dalam berbagai bidang, seperti matematika, fisika, dan teknik. Rumus ini digunakan untuk menghitung volume benda-benda berbentuk kubus, seperti balok, kotak, dan dadu. Selain itu, rumus ini juga digunakan dalam perhitungan kapasitas wadah berbentuk kubus, seperti tangki air dan akuarium.
Rumus volume kubus ditemukan oleh matematikawan Yunani kuno, Euclid, sekitar abad ke-3 SM. Rumus ini telah digunakan selama berabad-abad untuk menghitung volume benda-benda berbentuk kubus dan masih menjadi rumus yang penting hingga saat ini.
Rumus Volume Kubus
Rumus volume kubus adalah persamaan matematika yang digunakan untuk menghitung volume kubus, yaitu bangun ruang tiga dimensi dengan enam sisi berbentuk persegi. Rumus ini sangat penting dalam berbagai bidang, dan memiliki beberapa aspek penting, antara lain:
- Definisi: V = s3, di mana V adalah volume kubus dan s adalah panjang rusuk kubus.
- Aplikasi: Menghitung volume benda-benda berbentuk kubus, seperti balok, kotak, dan dadu.
- Sejarah: Ditemukan oleh matematikawan Yunani kuno, Euclid, sekitar abad ke-3 SM.
- Relevansi: Digunakan dalam berbagai bidang, seperti matematika, fisika, dan teknik.
Rumus volume kubus tidak hanya penting untuk menghitung volume benda-benda berbentuk kubus, tetapi juga memiliki keterkaitan dengan konsep matematika lainnya. Misalnya, rumus ini dapat digunakan untuk menghitung volume balok dengan cara mengalikan panjang, lebar, dan tinggi balok. Selain itu, rumus volume kubus juga dapat digunakan untuk menghitung luas permukaan kubus dengan cara mengalikan luas salah satu sisinya dengan 6.
Definisi
Persamaan ini menjelaskan hubungan mendasar antara volume kubus dan panjang rusuknya. Volume (V) suatu kubus berbanding lurus dengan pangkat tiga panjang rusuknya (s). Artinya, jika panjang rusuk suatu kubus dikalikan dengan suatu faktor, maka volume kubus tersebut akan dikalikan dengan pangkat tiga dari faktor tersebut.
-
Menghitung Volume Kubus:
Rumus ini memberikan cara langsung untuk menghitung volume kubus. Dengan mengetahui panjang rusuknya, kita dapat dengan mudah menghitung volumenya menggunakan persamaan V = s3. -
Hubungan dengan Bangun Ruang Lain:
Rumus volume kubus juga dapat digunakan untuk menghitung volume bangun ruang lain yang terkait dengan kubus. Misalnya, volume balok dapat dihitung dengan mengalikan panjang, lebar, dan tingginya, yang pada dasarnya merupakan tiga panjang rusuk dari sebuah kubus. -
Aplikasi dalam Kehidupan Nyata:
Rumus volume kubus memiliki banyak aplikasi dalam kehidupan nyata, seperti menghitung volume tangki air, akuarium, atau kotak penyimpanan. Dengan mengetahui volume benda-benda ini, kita dapat menentukan kapasitas atau jumlah ruang yang dapat ditampungnya. -
Dasar untuk Konsep Matematika Lanjutan:
Rumus volume kubus merupakan dasar untuk konsep matematika yang lebih kompleks, seperti menghitung volume bangun ruang komposit dan integral volume. Memahami rumus ini sangat penting untuk membangun pemahaman yang kuat tentang geometri dan kalkulus.
Secara keseluruhan, definisi V = s3 tidak hanya memberikan rumus untuk menghitung volume kubus, tetapi juga menyoroti hubungan mendasar antara volume dan dimensi kubus. Rumus ini memiliki aplikasi luas dalam berbagai bidang dan merupakan dasar untuk eksplorasi matematika yang lebih lanjut.
Aplikasi
Rumus volume kubus tidak hanya berguna untuk menghitung volume kubus itu sendiri, tetapi juga dapat diaplikasikan untuk menghitung volume benda-benda lain yang memiliki bentuk terkait dengan kubus, seperti balok, kotak, dan dadu.
-
Balok
Balok adalah bangun ruang yang memiliki enam sisi berbentuk persegi panjang. Volume balok dapat dihitung dengan mengalikan panjang, lebar, dan tingginya. Karena panjang, lebar, dan tinggi balok pada dasarnya adalah panjang rusuk dari sebuah kubus, maka rumus volume kubus (V = s3) dapat digunakan untuk menghitung volume balok. -
Kotak
Kotak adalah benda tiga dimensi yang memiliki enam sisi berbentuk persegi atau persegi panjang. Sama seperti balok, volume kotak dapat dihitung dengan mengalikan panjang, lebar, dan tingginya. Sekali lagi, rumus volume kubus dapat diterapkan karena panjang, lebar, dan tinggi kotak merupakan panjang rusuk dari sebuah kubus. -
Dadu
Dadu adalah sebuah kubus dengan enam sisi yang masing-masing diberi angka. Volume dadu dapat dengan mudah dihitung menggunakan rumus volume kubus, karena dadu pada dasarnya adalah sebuah kubus.
Dengan memahami hubungan antara rumus volume kubus dan bentuk-bentuk terkait, kita dapat memperluas aplikasi rumus ini untuk menghitung volume berbagai benda dalam kehidupan nyata, seperti kotak penyimpanan, akuarium, dan banyak lagi.
Sejarah
Penemuan rumus volume kubus oleh Euclid merupakan tonggak penting dalam sejarah matematika. Rumus ini tidak hanya memberikan metode untuk menghitung volume kubus, tetapi juga menjadi dasar untuk pengembangan konsep geometri dan kalkulus yang lebih kompleks.
Sebelum penemuan Euclid, tidak ada rumus yang jelas untuk menghitung volume kubus. Orang-orang pada waktu itu menggunakan metode coba-coba dan perkiraan untuk menentukan volume benda-benda berbentuk kubus. Penemuan Euclid memberikan solusi yang akurat dan dapat diandalkan untuk masalah ini, sehingga sangat memajukan pemahaman tentang geometri.
Selain memberikan metode perhitungan, rumus volume kubus juga memiliki signifikansi praktis. Rumus ini memungkinkan orang untuk menghitung volume benda-benda nyata berbentuk kubus, seperti balok, kotak, dan dadu. Hal ini sangat penting dalam berbagai bidang, seperti konstruksi, teknik, dan perdagangan.
Memahami sejarah penemuan rumus volume kubus membantu kita menghargai pentingnya matematika dan kontribusi para matematikawan kuno terhadap perkembangan ilmu pengetahuan. Rumus ini terus menjadi alat penting dalam berbagai bidang hingga saat ini, membuktikan nilai abadi dari penemuan Euclid.
Relevansi
Rumus volume kubus memiliki relevansi yang luas karena penggunaannya dalam berbagai bidang. Hubungannya dengan matematika, fisika, dan teknik sangat penting untuk memahami peran dan implikasinya dalam kehidupan nyata.
-
Matematika
Dalam matematika, rumus volume kubus merupakan dasar untuk menghitung volume bangun ruang lain, seperti balok dan prisma. Rumus ini juga digunakan dalam kalkulus untuk menghitung integral volume benda-benda beraturan dan tidak beraturan. -
Fisika
Dalam fisika, rumus volume kubus digunakan untuk menghitung volume benda-benda seperti kubus logam, balok kayu, dan tangki air. Volume ini penting untuk menentukan massa, kepadatan, dan sifat fisik lainnya dari benda-benda tersebut. -
Teknik
Dalam teknik, rumus volume kubus digunakan dalam desain dan konstruksi. Insinyur menggunakan rumus ini untuk menghitung volume beton yang dibutuhkan untuk membuat struktur seperti jembatan, gedung, dan bendungan. Rumus ini juga digunakan untuk menghitung kapasitas tangki penyimpanan, pipa, dan wadah lainnya.
Dengan memahami relevansi rumus volume kubus dalam berbagai bidang, kita dapat menghargai pentingnya rumus ini dalam pengembangan ilmu pengetahuan dan teknologi. Rumus ini tidak hanya sekadar persamaan matematika, tetapi juga alat yang ampuh untuk memecahkan masalah dan merancang solusi dalam dunia nyata.
Pertanyaan Umum tentang Rumus Volume Kubus
Berikut ini adalah beberapa pertanyaan umum yang sering diajukan terkait rumus volume kubus:
Pertanyaan 1: Kenapa rumus volume kubus menggunakan pangkat tiga dari panjang rusuk?
Jawaban: Rumus volume kubus (V = s3) menggunakan pangkat tiga karena volume kubus bergantung pada tiga dimensi, yaitu panjang, lebar, dan tinggi. Ketiga dimensi ini sama dengan panjang rusuk kubus (s). Oleh karena itu, volume kubus berbanding lurus dengan pangkat tiga dari panjang rusuknya.
Pertanyaan 2: Bagaimana cara menggunakan rumus volume kubus untuk menghitung volume balok?
Jawaban: Meskipun rumus volume kubus khusus untuk kubus, rumus ini juga dapat digunakan untuk menghitung volume balok karena balok dapat dianggap sebagai kubus yang memanjang. Untuk menghitung volume balok, cukup kalikan panjang, lebar, dan tinggi balok, yang semuanya mewakili panjang rusuk kubus.
Pertanyaan 3: Apa saja aplikasi rumus volume kubus dalam kehidupan nyata?
Jawaban: Rumus volume kubus memiliki banyak aplikasi dalam kehidupan nyata, antara lain:
- Menghitung volume akuarium untuk menentukan jumlah air yang dibutuhkan
- Menghitung volume balok beton untuk konstruksi
- Menentukan kapasitas tangki penyimpanan untuk cairan atau bahan curah
- Membandingkan volume benda-benda berbentuk kubus untuk menentukan mana yang lebih besar
Pertanyaan 4: Siapa yang menemukan rumus volume kubus?
Jawaban: Rumus volume kubus ditemukan oleh matematikawan Yunani kuno, Euclid, sekitar abad ke-3 SM. Penemuan ini menjadi tonggak penting dalam perkembangan geometri dan memberikan dasar untuk menghitung volume benda-benda berbentuk kubus.
Memahami rumus volume kubus sangat penting untuk berbagai aplikasi dalam matematika, fisika, teknik, dan kehidupan sehari-hari. Dengan mempelajari rumus ini dan prinsip-prinsip yang mendasarinya, kita dapat memecahkan masalah dan membuat perhitungan yang akurat terkait dengan benda-benda berbentuk kubus.
Tips Menghitung Volume Kubus:
Saat menggunakan rumus volume kubus, perhatikan beberapa tips berikut:
- Pastikan satuan panjang yang digunakan konsisten (misalnya, semua dalam sentimeter atau meter)
- Jika panjang rusuk kubus diberikan dalam satuan yang berbeda, konversikan ke satuan yang sama sebelum menghitung volume
- Untuk balok, ingatlah untuk mengalikan panjang, lebar, dan tinggi, yang semuanya mewakili panjang rusuk kubus
Dengan mengikuti tips ini, Anda dapat menghitung volume kubus dan benda-benda terkait secara akurat dan efisien.
Tips Menghitung Volume Kubus
Berikut adalah beberapa tips untuk menghitung volume kubus secara akurat dan efisien:
Tip 1: Konsistensi Satuan Panjang
Pastikan satuan panjang yang digunakan konsisten. Artinya, jika panjang rusuk kubus diberikan dalam sentimeter, maka volume juga harus dinyatakan dalam sentimeter kubik. Menggunakan satuan yang berbeda dapat menyebabkan kesalahan perhitungan.
Tip 2: Konversi Satuan
Jika panjang rusuk kubus diberikan dalam satuan yang berbeda, seperti meter atau inci, konversikan ke satuan yang sama sebelum menghitung volume. Hal ini penting untuk memastikan bahwa perhitungan dilakukan dengan benar.
Tip 3: Identifikasi Rusuk Kubus
Untuk menghitung volume balok, ingatlah bahwa panjang, lebar, dan tinggi balok mewakili panjang rusuk kubus. Dengan demikian, mengalikan ketiga nilai tersebut akan menghasilkan volume balok yang ekuivalen dengan volume kubus.
Tip 4: Akurasi Perhitungan
Lakukan perhitungan dengan hati-hati dan periksa kembali hasilnya untuk memastikan akurasinya. Jika memungkinkan, gunakan kalkulator untuk menghindari kesalahan perhitungan manual.
Dengan mengikuti tips ini, Anda dapat menghitung volume kubus dan benda-benda terkait dengan lebih akurat dan efisien.










