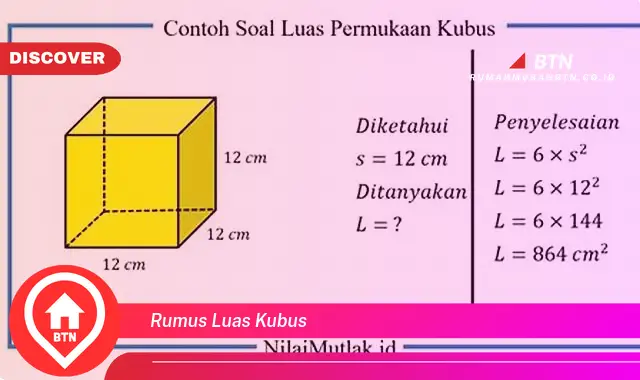
Rumus luas kubus adalah persamaan matematika yang digunakan untuk menghitung luas permukaan kubus. Kubus adalah bangun ruang tiga dimensi yang memiliki enam sisi berbentuk persegi, dan semua sisinya memiliki panjang yang sama. Rumus luas kubus dapat digunakan dalam berbagai aplikasi, seperti menghitung luas permukaan kubus yang digunakan dalam kemasan atau konstruksi, menghitung volume kubus, dan menyelesaikan masalah geometri.
Rumus luas kubus sangat penting karena memungkinkan kita menghitung luas permukaan kubus dengan cepat dan mudah. Hal ini dapat berguna dalam berbagai situasi, seperti saat menghitung luas bahan yang dibutuhkan untuk menutupi kubus atau menghitung volume benda yang berbentuk kubus. Selain itu, rumus luas kubus juga memiliki signifikansi historis karena telah digunakan selama berabad-abad untuk memecahkan masalah geometri.
Di artikel ini, kita akan membahas secara lebih rinci tentang rumus luas kubus, termasuk cara menggunakannya, berbagai aplikasinya, dan sejarahnya. Kita juga akan membahas beberapa topik terkait, seperti cara menghitung volume kubus dan cara menyelesaikan masalah geometri yang melibatkan kubus.
Rumus Luas Kubus
Rumus luas kubus sangat penting karena memiliki berbagai aplikasi dan signifikansi historis. Berikut adalah empat aspek kunci dari rumus luas kubus:
- Definisi: Persamaan matematika untuk menghitung luas permukaan kubus.
- Aplikasi: Menghitung luas permukaan dan volume kubus, menyelesaikan masalah geometri.
- Sejarah: Digunakan selama berabad-abad untuk memecahkan masalah geometri.
- Rumus: L = 6 x s, di mana L adalah luas permukaan dan s adalah panjang sisi kubus.
Keempat aspek ini saling terkait dan membentuk pemahaman yang komprehensif tentang rumus luas kubus. Definisi memberikan dasar untuk memahami konsep tersebut, sementara aplikasi menunjukkan relevansinya dalam berbagai bidang. Sejarah menggarisbawahi pentingnya historis rumus tersebut, dan rumus itu sendiri memberikan alat praktis untuk menghitung luas permukaan kubus.
Sebagai contoh, rumus luas kubus dapat digunakan untuk menghitung luas permukaan kubus yang digunakan sebagai kemasan. Dengan mengetahui luas permukaan, produsen dapat menentukan jumlah bahan yang dibutuhkan untuk menutupi kubus dan memastikan bahwa produk dilindungi dengan baik. Selain itu, rumus luas kubus juga dapat digunakan untuk menghitung volume kubus, yang penting untuk menentukan kapasitas atau isi benda yang berbentuk kubus.
Secara keseluruhan, rumus luas kubus adalah alat penting yang memiliki berbagai aplikasi dalam geometri dan bidang lainnya. Dengan memahami definisi, aplikasi, sejarah, dan rumus itu sendiri, kita dapat memperoleh apresiasi yang lebih dalam tentang pentingnya dan relevansinya.
Definisi
Definisi rumus luas kubus sebagai persamaan matematika sangat penting karena memberikan dasar untuk memahami konsep tersebut. Persamaan ini memungkinkan kita menghitung luas permukaan kubus dengan jelas dan sistematis, menjadikannya alat yang ampuh untuk menyelesaikan masalah geometri dan aplikasi praktis lainnya.
Sebagai komponen rumus luas kubus, definisi ini menetapkan kerangka kerja untuk menghitung luas permukaan kubus. Ini memberikan pemahaman tentang apa yang diwakili oleh rumus dan bagaimana rumus tersebut dapat digunakan untuk memecahkan masalah. Tanpa definisi yang jelas, rumus luas kubus hanya akan menjadi serangkaian simbol tanpa makna atau tujuan yang jelas.
Dalam praktiknya, definisi rumus luas kubus memungkinkan kita menerapkannya dalam berbagai situasi. Misalnya, dalam konstruksi, definisi ini digunakan untuk menentukan jumlah bahan yang dibutuhkan untuk menutupi kubus, seperti saat menghitung luas permukaan kubus yang digunakan sebagai kemasan. Dalam geometri, definisi ini digunakan untuk menyelesaikan masalah yang melibatkan menghitung luas permukaan dan volume kubus.
Secara keseluruhan, definisi rumus luas kubus sebagai persamaan matematika sangat penting karena memberikan dasar untuk memahami konsep, menerapkannya dalam praktik, dan menyelesaikan berbagai masalah geometri dan aplikasi praktis lainnya.
Aplikasi
Rumus luas kubus memiliki berbagai aplikasi dalam geometri dan bidang lainnya, terutama dalam menghitung luas permukaan dan volume kubus, serta menyelesaikan masalah geometri. Aplikasi-aplikasi ini menyoroti pentingnya dan relevansinya dalam kehidupan nyata.
- Menghitung luas permukaan: Rumus luas kubus digunakan untuk menghitung luas permukaan kubus, yaitu jumlah luas semua sisinya. Aplikasi ini penting dalam berbagai bidang, seperti konstruksi, pengemasan, dan desain.
- Menghitung volume: Rumus luas kubus juga dapat digunakan untuk menghitung volume kubus, yaitu ruang yang ditempati oleh kubus. Aplikasi ini penting dalam bidang-bidang seperti arsitektur, teknik, dan matematika.
- Memecahkan masalah geometri: Rumus luas kubus dapat digunakan untuk menyelesaikan berbagai masalah geometri yang melibatkan kubus. Misalnya, rumus ini dapat digunakan untuk menentukan panjang diagonal kubus atau menghitung luas permukaan prisma yang alasnya berbentuk kubus.
Aplikasi-aplikasi ini menunjukkan bahwa rumus luas kubus adalah alat yang serbaguna dan penting dalam berbagai bidang. Memahami aplikasi-aplikasi ini membantu kita mengapresiasi pentingnya dan relevansinya dalam kehidupan nyata.
Sejarah
Rumus luas kubus memiliki sejarah panjang yang berkaitan dengan pemecahan masalah geometri. Sejak zaman dahulu, para ahli matematika dan ilmuwan telah menggunakan rumus ini untuk menghitung luas permukaan dan volume kubus, serta menyelesaikan berbagai masalah geometri.
- Penggunaan dalam Arsitektur dan Teknik: Rumus luas kubus telah digunakan dalam arsitektur dan teknik selama berabad-abad untuk merancang dan membangun struktur yang melibatkan kubus. Misalnya, rumus ini digunakan untuk menentukan luas permukaan dinding dan lantai bangunan berbentuk kubus, serta untuk menghitung volume ruang yang berbentuk kubus.
- Pembangunan Piramida: Di Mesir kuno, rumus luas kubus kemungkinan besar digunakan dalam pembangunan piramida, yang merupakan struktur berbentuk kubus raksasa. Para pembangun piramida menggunakan rumus ini untuk menghitung luas permukaan dan volume piramida, serta untuk menentukan jumlah bahan yang dibutuhkan untuk membangunnya.
- Perkembangan Matematika: Rumus luas kubus juga memainkan peran penting dalam perkembangan matematika. Ahli matematika Yunani kuno, seperti Euclid, menggunakan rumus ini dalam karyanya tentang geometri. Rumus ini juga digunakan dalam pengembangan kalkulus dan aljabar.
Sejarah panjang penggunaan rumus luas kubus dalam pemecahan masalah geometri menunjukkan pentingnya dan relevansinya yang berkelanjutan. Rumus ini telah menjadi alat penting bagi para ahli matematika, ilmuwan, arsitek, dan insinyur selama berabad-abad, dan terus digunakan hingga saat ini untuk menyelesaikan berbagai masalah geometri dan aplikasi praktis lainnya.
Rumus
Rumus L = 6 x s merupakan persamaan matematika untuk menghitung luas permukaan kubus, di mana L adalah luas permukaan dan s adalah panjang sisi kubus. Rumus ini sangat penting dalam geometri karena memungkinkan kita menghitung luas permukaan kubus dengan mudah dan akurat.
- Menghitung Luas Permukaan: Rumus L = 6 x s digunakan untuk menghitung luas permukaan kubus, yaitu jumlah luas semua sisinya. Aplikasi ini penting dalam berbagai bidang, seperti konstruksi, pengemasan, dan desain.
- Menghitung Volume: Rumus L = 6 x s juga dapat digunakan untuk menghitung volume kubus, yaitu ruang yang ditempati oleh kubus. Aplikasi ini penting dalam bidang-bidang seperti arsitektur, teknik, dan matematika.
- Menyelesaikan Masalah Geometri: Rumus L = 6 x s dapat digunakan untuk menyelesaikan berbagai masalah geometri yang melibatkan kubus. Misalnya, rumus ini dapat digunakan untuk menentukan panjang diagonal kubus atau menghitung luas permukaan prisma yang alasnya berbentuk kubus.
Rumus L = 6 x s merupakan bagian penting dari rumus luas kubus karena menyediakan alat praktis untuk menghitung luas permukaan kubus. Rumus ini memiliki berbagai aplikasi dalam geometri dan bidang lainnya, menjadikannya alat yang sangat berharga untuk menyelesaikan masalah dan membuat perhitungan yang akurat.
Tanya Jawab Umum
Bagian Tanya Jawab Umum ini dirancang untuk memberikan informasi tambahan dan klarifikasi terkait topik rumus luas kubus. Kami telah menyusun beberapa pertanyaan umum yang mungkin Anda miliki, beserta jawabannya yang informatif.
Pertanyaan 1: Apa saja contoh aplikasi rumus luas kubus dalam kehidupan nyata?
Rumus luas kubus memiliki banyak aplikasi dalam kehidupan nyata, seperti menghitung luas permukaan kubus untuk menentukan jumlah bahan yang dibutuhkan untuk menutupinya, menghitung volume kubus untuk menentukan kapasitasnya, dan menyelesaikan masalah geometri yang melibatkan kubus.
Pertanyaan 2: Apakah rumus luas kubus hanya berlaku untuk kubus dengan ukuran yang sama?
Ya, rumus luas kubus hanya berlaku untuk kubus dengan ukuran yang sama pada keenam sisinya. Jika kubus memiliki sisi dengan panjang yang berbeda, maka rumus luas kubus tidak dapat digunakan untuk menghitung luas permukaannya.
Pertanyaan 3: Bagaimana cara menggunakan rumus luas kubus untuk menghitung volume kubus?
Rumus luas kubus tidak dapat digunakan secara langsung untuk menghitung volume kubus. Untuk menghitung volume kubus, Anda perlu menggunakan rumus volume kubus, yaitu V = s, di mana V adalah volume dan s adalah panjang sisi kubus.
Pertanyaan 4: Mengapa rumus luas kubus penting dalam matematika?
Rumus luas kubus adalah rumus penting dalam matematika karena memungkinkan kita untuk menghitung luas permukaan kubus dengan mudah dan akurat. Rumus ini digunakan dalam berbagai bidang, seperti geometri, arsitektur, dan teknik, untuk menyelesaikan masalah dan membuat perhitungan yang akurat.
Kami harap Tanya Jawab Umum ini bermanfaat. Jika Anda memiliki pertanyaan tambahan, jangan ragu untuk bertanya kepada ahli atau mencari sumber informasi lainnya.
Mari beralih ke artikel Tips untuk mempelajari lebih lanjut tentang penggunaan rumus luas kubus secara efektif.
Tips Mempelajari Rumus Luas Kubus
Mempelajari rumus luas kubus dengan efektif sangat penting untuk menyelesaikan masalah geometri dan aplikasi praktis lainnya. Berikut adalah beberapa tips untuk membantu Anda menguasai rumus ini:
Tip 1: Pahami Konsep Kubus
Sebelum mempelajari rumus luas kubus, penting untuk memahami konsep kubus itu sendiri. Kubus adalah bangun ruang tiga dimensi yang memiliki enam sisi berbentuk persegi, dan semua sisinya memiliki panjang yang sama. Memahami konsep ini akan membantu Anda memvisualisasikan rumus dan menerapkannya dengan benar.
Tip 2: Hafalkan Rumus
Rumus luas kubus adalah L = 6 x s, di mana L adalah luas permukaan dan s adalah panjang sisi kubus. Hafalkan rumus ini dengan baik agar Anda dapat menggunakannya dengan mudah saat dibutuhkan. Anda dapat menggunakan teknik menghafal seperti pengulangan, kartu catatan, atau lagu untuk membantu Anda mengingat rumus.
Tip 3: Berlatih Soal
Setelah Anda memahami rumus luas kubus, berlatihlah soal sebanyak mungkin. Ini akan membantu Anda meningkatkan keterampilan dalam menggunakan rumus dan meningkatkan pemahaman Anda tentang konsep yang mendasarinya. Anda dapat menemukan soal latihan di buku teks, soal ujian, atau sumber online.
Tip 4: Terapkan dalam Konteks
Untuk memperkuat pemahaman Anda tentang rumus luas kubus, cobalah terapkan dalam konteks kehidupan nyata. Misalnya, Anda dapat menggunakan rumus untuk menghitung luas permukaan kubus yang digunakan sebagai kemasan atau menghitung volume kubus yang digunakan sebagai akuarium. Menerapkan rumus dalam konteks akan membantu Anda melihat relevansinya dan meningkatkan kemampuan pemecahan masalah Anda.
Dengan mengikuti tips ini, Anda dapat mempelajari rumus luas kubus secara efektif dan meningkatkan keterampilan Anda dalam menyelesaikan masalah geometri yang melibatkan kubus.










