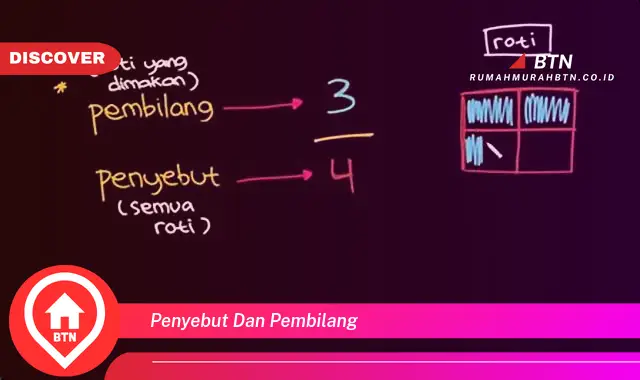
Penyebut dan pembilang adalah dua istilah penting dalam matematika, khususnya dalam operasi pecahan. Penyebut merujuk pada angka yang terletak di bagian bawah pecahan, sedangkan pembilang merujuk pada angka yang terletak di bagian atas pecahan.
Memahami konsep penyebut dan pembilang sangat penting untuk melakukan operasi matematika dasar seperti penjumlahan, pengurangan, perkalian, dan pembagian pecahan. Selain itu, penyebut dan pembilang juga memainkan peran penting dalam menyederhanakan pecahan dan mengubahnya menjadi bentuk desimal.
Dalam artikel ini, kita akan membahas lebih dalam tentang penyebut dan pembilang, termasuk definisi, sifat, operasi, dan aplikasinya dalam berbagai bidang matematika.
Penyebut dan Pembilang
Dalam matematika, penyebut dan pembilang merupakan dua komponen penting dari pecahan. Penyebut terletak di bagian bawah pecahan dan menunjukkan jumlah bagian yang sama dari keseluruhan, sedangkan pembilang terletak di bagian atas pecahan dan menunjukkan banyaknya bagian yang diambil.
- Fungsi: Menunjukkan nilai dan operasi pecahan
- Operasi: Penjumlahan, pengurangan, perkalian, dan pembagian
- Sifat: Dapat disederhanakan dan diubah menjadi bentuk desimal
- Aplikasi: Digunakan dalam berbagai bidang, seperti pengukuran, geometri, dan statistika
Memahami penyebut dan pembilang sangat penting untuk menguasai operasi pecahan dan konsep matematika lainnya. Dengan memahami hubungan antara penyebut dan pembilang, kita dapat menyelesaikan masalah matematika dengan lebih mudah dan akurat. Misalnya, kita dapat menyederhanakan pecahan 6/12 menjadi 1/2 dengan membagi penyebut dan pembilang dengan 6. Kita juga dapat menjumlahkan pecahan 1/4 dan 1/2 dengan mencari penyebut yang sama (4) dan kemudian menjumlahkan pembilangnya (1 + 2 = 3), sehingga hasilnya adalah 3/4.
Fungsi
Penyebut dan pembilang memainkan peran penting dalam menentukan nilai dan operasi pecahan. Penyebut menunjukkan banyaknya bagian yang sama dari keseluruhan, sedangkan pembilang menunjukkan banyaknya bagian yang diambil. Dengan memahami hubungan antara penyebut dan pembilang, kita dapat melakukan operasi matematika pada pecahan dengan mudah dan akurat.
-
Menentukan Nilai Pecahan
Nilai pecahan ditentukan oleh perbandingan antara pembilang dan penyebut. Misalnya, pecahan 1/2 menunjukkan bahwa satu bagian dari dua bagian yang sama diambil. Semakin besar penyebutnya, semakin kecil nilai pecahannya, dan sebaliknya. -
Operasi Penjumlahan dan Pengurangan
Untuk menjumlahkan atau mengurangkan pecahan, kita perlu mencari penyebut yang sama terlebih dahulu. Setelah penyebutnya sama, kita dapat menjumlahkan atau mengurangkan pembilangnya saja. -
Operasi Perkalian
Untuk mengalikan pecahan, kita cukup mengalikan pembilang dengan pembilang dan penyebut dengan penyebut. Misalnya, (1/2) x (3/4) = (1 x 3) / (2 x 4) = 3/8. -
Operasi Pembagian
Untuk membagi pecahan, kita cukup membalik pecahan kedua (penyebut dan pembilangnya ditukar) dan kemudian mengalikannya dengan pecahan pertama. Misalnya, (1/2) : (3/4) = (1/2) x (4/3) = 2/3.
Dengan memahami fungsi penyebut dan pembilang dalam menunjukkan nilai dan operasi pecahan, kita dapat menyelesaikan berbagai masalah matematika dengan lebih mudah dan akurat.
Operasi
Dalam matematika, operasi penjumlahan, pengurangan, perkalian, dan pembagian merupakan operasi dasar yang dilakukan pada bilangan, termasuk pecahan. Penyebut dan pembilang memainkan peran penting dalam menentukan hasil operasi tersebut.
Untuk melakukan operasi penjumlahan dan pengurangan pada pecahan, penyebutnya harus sama. Jika penyebutnya berbeda, maka pecahan tersebut harus diubah terlebih dahulu menjadi pecahan yang senilai dengan penyebut yang sama. Misalnya, untuk menjumlahkan pecahan 1/2 dan 1/4, kita perlu mengubah 1/4 menjadi 2/8 agar penyebutnya sama. Setelah penyebutnya sama, kita dapat menjumlahkan atau mengurangkan pembilangnya saja.
Untuk operasi perkalian dan pembagian pada pecahan, kita cukup mengalikan atau membagi pembilang dan penyebutnya secara langsung. Misalnya, untuk mengalikan pecahan 1/2 dengan 3/4, kita cukup mengalikan pembilang dengan pembilang dan penyebut dengan penyebut, sehingga hasilnya adalah 3/8. Begitu juga untuk operasi pembagian, kita cukup membagi pembilang dengan pembilang dan penyebut dengan penyebut.
Memahami hubungan antara operasi penjumlahan, pengurangan, perkalian, dan pembagian dengan penyebut dan pembilang sangat penting untuk menyelesaikan berbagai masalah matematika. Operasi-operasi ini banyak digunakan dalam kehidupan sehari-hari, seperti dalam pengukuran, geometri, dan statistika.
Sifat
Penyebut dan pembilang memiliki sifat yang penting, yaitu dapat disederhanakan dan diubah menjadi bentuk desimal. Sifat ini sangat berguna dalam berbagai aplikasi matematika, seperti perhitungan, pengukuran, dan statistika.
-
Penyederhanaan Pecahan
Penyederhanaan pecahan dilakukan dengan membagi penyebut dan pembilang dengan faktor persekutuan terbesar (FPB) keduanya. Hasilnya adalah pecahan yang senilai dengan pecahan semula, tetapi dengan penyebut dan pembilang yang lebih kecil.
Contoh: Pecahan 6/12 dapat disederhanakan menjadi 1/2 karena FPB dari 6 dan 12 adalah 6. -
Pengubahan ke Bentuk Desimal
Pecahan dapat diubah menjadi bentuk desimal dengan cara membagi pembilang dengan penyebut. Hasilnya adalah angka desimal yang menyatakan nilai pecahan tersebut.
Contoh: Pecahan 1/2 dapat diubah menjadi bentuk desimal 0,5 karena 1 dibagi 2 sama dengan 0,5.
Sifat penyebut dan pembilang yang dapat disederhanakan dan diubah menjadi bentuk desimal sangat penting dalam berbagai aplikasi matematika. Dengan memahami sifat ini, kita dapat melakukan perhitungan dengan lebih mudah dan akurat, serta memahami hubungan antara pecahan dan angka desimal.
Aplikasi
Pemahaman tentang penyebut dan pembilang sangat penting dalam berbagai bidang matematika dan sains. Konsep ini menjadi dasar untuk menyelesaikan masalah di bidang berikut:
-
Pengukuran
Dalam pengukuran, penyebut dan pembilang digunakan untuk menyatakan besaran yang diukur. Misalnya, dalam pengukuran panjang, penyebut menyatakan satuan panjang (seperti cm atau m), sedangkan pembilang menyatakan nilai besaran yang diukur. -
Geometri
Dalam geometri, penyebut dan pembilang digunakan untuk menentukan luas, keliling, dan volume bangun ruang. Misalnya, dalam menghitung luas persegi panjang, penyebut menyatakan panjang persegi panjang, sedangkan pembilang menyatakan lebar persegi panjang. -
Statistika
Dalam statistika, penyebut dan pembilang digunakan untuk menghitung nilai rata-rata, median, dan modus suatu data. Misalnya, dalam menghitung nilai rata-rata, penyebut menyatakan banyaknya data, sedangkan pembilang menyatakan jumlah seluruh data.
Dengan memahami konsep penyebut dan pembilang, kita dapat lebih mudah menyelesaikan masalah dan menarik kesimpulan dari data yang disajikan dalam bentuk pecahan.
Pertanyaan Umum tentang Penyebut dan Pembilang
Bagian ini berisi pertanyaan umum dan jawabannya tentang konsep penyebut dan pembilang dalam matematika.
Pertanyaan 1: Apa fungsi penyebut dan pembilang dalam pecahan?
Penyebut menunjukkan banyaknya bagian yang sama dari keseluruhan, sedangkan pembilang menunjukkan banyaknya bagian yang diambil. Keduanya bersama-sama menentukan nilai dan operasi pecahan.
Pertanyaan 2: Bagaimana cara melakukan operasi matematika pada pecahan?
Untuk menjumlahkan atau mengurangkan pecahan, penyebutnya harus sama. Untuk mengalikan pecahan, kalikan pembilang dengan pembilang dan penyebut dengan penyebut. Untuk membagi pecahan, balik pecahan kedua dan kalikan dengan pecahan pertama.
Pertanyaan 3: Apa pentingnya memahami penyederhanaan pecahan?
Penyederhanaan pecahan membantu kita mendapatkan pecahan yang senilai dengan pecahan semula, tetapi dengan penyebut dan pembilang yang lebih kecil. Hal ini memudahkan perhitungan dan perbandingan pecahan.
Pertanyaan 4: Di bidang apa saja penyebut dan pembilang digunakan?
Penyebut dan pembilang digunakan dalam berbagai bidang matematika, seperti pengukuran, geometri, dan statistika, serta dalam aplikasi sehari-hari seperti perhitungan dan pengukuran.
Dengan memahami konsep penyebut dan pembilang, kita dapat lebih mudah menyelesaikan masalah dan memahami konsep matematika yang lebih kompleks.
Mari beralih ke bagian selanjutnya yang akan membahas tips dalam menguasai konsep penyebut dan pembilang.
Tips Menguasai Konsep Penyebut dan Pembilang
Memahami konsep penyebut dan pembilang sangat penting dalam matematika. Berikut adalah beberapa tips yang dapat membantu Anda menguasai konsep ini:
Tip 1: Pahami Fungsi dan Makna Penyebut dan Pembilang
Penyebut menunjukkan banyaknya bagian yang sama dari keseluruhan, sedangkan pembilang menunjukkan banyaknya bagian yang diambil. Penting untuk memahami konsep ini sebelum melakukan operasi matematika pada pecahan.
Tip 2: Latih Operasi Matematika pada Pecahan
Latihan yang teratur sangat penting untuk menguasai operasi matematika pada pecahan. Cobalah untuk menjumlahkan, mengurangkan, mengalikan, dan membagi pecahan dengan penyebut yang berbeda.
Tip 3: Kuasai Penyederhanaan Pecahan
Penyederhanaan pecahan membantu menyederhanakan pecahan ke bentuk yang lebih sederhana. Latihlah mencari faktor persekutuan terbesar (FPB) dari penyebut dan pembilang untuk menyederhanakan pecahan.
Tip 4: Terapkan Konsep dalam Berbagai Bidang
Konsep penyebut dan pembilang digunakan dalam berbagai bidang, seperti pengukuran, geometri, dan statistika. Cobalah untuk menerapkan konsep ini dalam soal-soal dari berbagai bidang untuk memperkuat pemahaman Anda.
Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman Anda tentang konsep penyebut dan pembilang, sehingga memudahkan Anda dalam menyelesaikan masalah matematika dan memahami konsep matematika yang lebih kompleks.










