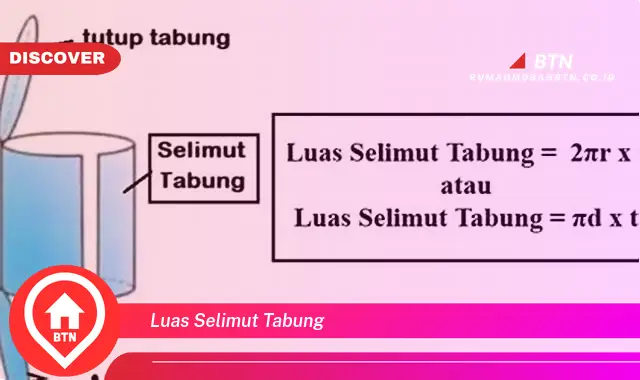
Luas selimut tabung adalah besaran yang menyatakan ukuran permukaan tabung yang melengkung. Rumus luas selimut tabung adalah L = 2r x t, di mana r adalah jari-jari alas tabung dan t adalah tinggi tabung.
Luas selimut tabung penting dalam berbagai bidang, seperti matematika, fisika, dan teknik. Dalam matematika, luas selimut tabung digunakan untuk menghitung volume tabung. Dalam fisika, luas selimut tabung digunakan untuk menghitung gaya yang bekerja pada benda yang bergerak dalam fluida. Dalam teknik, luas selimut tabung digunakan untuk menghitung luas permukaan pipa dan tangki.
Konsep luas selimut tabung telah dikenal sejak zaman kuno. Bangsa Mesir kuno menggunakan rumus luas selimut tabung untuk menghitung volume gulungan papirus. Bangsa Yunani kuno menggunakan rumus luas selimut tabung untuk menghitung volume bejana berbentuk tabung.
Luas Selimut Tabung
Luas selimut tabung merupakan besaran penting yang digunakan dalam berbagai bidang. Berikut adalah 4 aspek penting yang berkaitan dengan luas selimut tabung:
- Rumus
- Aplikasi
- Sejarah
- Contoh
Rumus luas selimut tabung adalah L = 2r x t, di mana r adalah jari-jari alas tabung dan t adalah tinggi tabung. Rumus ini digunakan untuk menghitung luas permukaan tabung yang melengkung. Luas selimut tabung memiliki banyak aplikasi dalam bidang matematika, fisika, dan teknik. Dalam matematika, luas selimut tabung digunakan untuk menghitung volume tabung. Dalam fisika, luas selimut tabung digunakan untuk menghitung gaya yang bekerja pada benda yang bergerak dalam fluida. Dalam teknik, luas selimut tabung digunakan untuk menghitung luas permukaan pipa dan tangki.
Konsep luas selimut tabung telah dikenal sejak zaman kuno. Bangsa Mesir kuno menggunakan rumus luas selimut tabung untuk menghitung volume gulungan papirus. Bangsa Yunani kuno menggunakan rumus luas selimut tabung untuk menghitung volume bejana berbentuk tabung. Contoh penerapan luas selimut tabung dalam kehidupan sehari-hari antara lain menghitung luas permukaan kaleng minuman, pipa saluran air, dan tangki penyimpanan.
Rumus
Rumus luas selimut tabung sangatlah penting karena memungkinkan kita menghitung luas permukaan tabung yang melengkung secara akurat. Tanpa rumus ini, kita tidak dapat menghitung volume tabung, gaya yang bekerja pada benda dalam fluida, atau luas permukaan pipa dan tangki. Dalam konteks yang lebih luas, rumus luas selimut tabung merupakan bagian penting dari matematika, fisika, dan teknik, memfasilitasi berbagai perhitungan dan aplikasi praktis.
Dalam kehidupan sehari-hari, rumus luas selimut tabung digunakan dalam berbagai aplikasi, seperti menghitung luas permukaan kaleng minuman, pipa saluran air, dan tangki penyimpanan. Pemahaman tentang rumus ini memungkinkan kita menyelesaikan masalah praktis yang melibatkan tabung, seperti menghitung jumlah cat yang dibutuhkan untuk mengecat tangki atau menghitung gaya yang bekerja pada benda yang bergerak dalam pipa.
Kesimpulannya, rumus luas selimut tabung merupakan alat penting yang digunakan dalam berbagai bidang. Dengan memahami rumus ini, kita dapat menyelesaikan masalah praktis yang melibatkan tabung dan memperoleh wawasan yang lebih dalam tentang sifat dan perilaku tabung.
Aplikasi
Luas selimut tabung memiliki banyak aplikasi dalam berbagai bidang. Berikut adalah beberapa contohnya:
-
Matematika
Dalam matematika, luas selimut tabung digunakan untuk menghitung volume tabung. Rumus untuk menghitung volume tabung adalah V = L x t, di mana V adalah volume tabung, L adalah luas selimut tabung, dan t adalah tinggi tabung. Contoh penerapan luas selimut tabung dalam matematika adalah menghitung volume kaleng minuman atau pipa saluran air.
-
Fisika
Dalam fisika, luas selimut tabung digunakan untuk menghitung gaya yang bekerja pada benda yang bergerak dalam fluida. Gaya yang bekerja pada benda tersebut adalah F = x v^2 x L, di mana F adalah gaya yang bekerja pada benda, adalah massa jenis fluida, v adalah kecepatan benda, dan L adalah luas selimut tabung yang terkena fluida. Contoh penerapan luas selimut tabung dalam fisika adalah menghitung gaya yang bekerja pada bola yang bergerak dalam air atau gaya yang bekerja pada sayap pesawat.
-
Teknik
Dalam teknik, luas selimut tabung digunakan untuk menghitung luas permukaan pipa dan tangki. Luas permukaan pipa atau tangki digunakan untuk menghitung jumlah bahan yang dibutuhkan untuk membuat pipa atau tangki tersebut. Contoh penerapan luas selimut tabung dalam teknik adalah menghitung luas permukaan pipa saluran air atau luas permukaan tangki penyimpanan air.
Dengan memahami luas selimut tabung dan rumusnya, kita dapat menyelesaikan berbagai masalah praktis yang melibatkan tabung dalam kehidupan sehari-hari. Pemahaman ini juga penting untuk berbagai bidang ilmu pengetahuan dan teknik.
Sejarah
Sejarah memiliki hubungan yang erat dengan perkembangan luas selimut tabung. Konsep luas selimut tabung telah dikenal sejak zaman kuno, dan seiring berjalannya waktu, konsep ini terus disempurnakan dan diaplikasikan dalam berbagai bidang.
Pada awalnya, konsep luas selimut tabung digunakan untuk menghitung volume gulungan papirus oleh bangsa Mesir kuno. Kemudian, bangsa Yunani kuno mengembangkan konsep ini lebih lanjut untuk menghitung volume bejana berbentuk tabung. Seiring kemajuan matematika, fisika, dan teknik, konsep luas selimut tabung terus digunakan dan disempurnakan untuk menyelesaikan berbagai masalah praktis.
Pemahaman tentang sejarah luas selimut tabung sangat penting karena memungkinkan kita untuk memahami bagaimana konsep ini berkembang dan diaplikasikan dalam berbagai bidang. Dengan memahami sejarah, kita dapat lebih mengapresiasi pentingnya konsep ini dan bagaimana konsep ini telah berkontribusi pada kemajuan ilmu pengetahuan dan teknologi.
Contoh
Contoh merupakan aspek penting dalam memahami luas selimut tabung. Dengan mengamati contoh-contoh nyata, kita dapat memahami konsep luas selimut tabung secara lebih konkret dan melihat penerapannya dalam kehidupan sehari-hari.
-
Contoh 1: Kaleng Minuman
Kaleng minuman merupakan contoh nyata dari tabung. Luas selimut tabung kaleng minuman dapat dihitung menggunakan rumus L = 2r x t, di mana r adalah jari-jari alas kaleng dan t adalah tinggi kaleng. Memahami luas selimut tabung kaleng minuman penting untuk menghitung luas permukaan kaleng dan memperkirakan jumlah cat yang dibutuhkan untuk mengecat kaleng tersebut.
-
Contoh 2: Pipa Saluran Air
Pipa saluran air juga merupakan contoh tabung. Luas selimut tabung pipa saluran air dapat dihitung menggunakan rumus yang sama dengan kaleng minuman. Memahami luas selimut tabung pipa saluran air penting untuk menghitung luas permukaan pipa dan memperkirakan jumlah bahan yang dibutuhkan untuk membuat pipa tersebut.
-
Contoh 3: Tangki Penyimpanan Air
Tangki penyimpanan air merupakan contoh lain dari tabung. Luas selimut tabung tangki penyimpanan air dapat dihitung menggunakan rumus yang sama dengan kaleng minuman dan pipa saluran air. Memahami luas selimut tabung tangki penyimpanan air penting untuk menghitung luas permukaan tangki dan memperkirakan jumlah bahan yang dibutuhkan untuk membuat tangki tersebut.
Dengan memahami contoh-contoh tersebut, kita dapat melihat bagaimana luas selimut tabung diterapkan dalam kehidupan nyata dan bagaimana konsep ini digunakan untuk menyelesaikan masalah praktis. Pemahaman tentang contoh-contoh ini juga penting untuk menguasai konsep luas selimut tabung secara keseluruhan.
Pertanyaan Umum Seputar Luas Selimut Tabung
Bagian ini akan membahas beberapa pertanyaan umum yang sering diajukan terkait dengan luas selimut tabung. Pertanyaan-pertanyaan ini akan dijawab secara informatif dan jelas untuk memberikan pemahaman yang lebih baik tentang topik ini.
Pertanyaan 1: Apa saja aplikasi luas selimut tabung dalam kehidupan sehari-hari?
Luas selimut tabung memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti menghitung luas permukaan kaleng minuman, pipa saluran air, dan tangki penyimpanan. Memahami luas selimut tabung penting untuk menyelesaikan berbagai masalah praktis yang melibatkan tabung.
Pertanyaan 2: Bagaimana cara menghitung luas selimut tabung?
Luas selimut tabung dapat dihitung menggunakan rumus L = 2r x t, di mana r adalah jari-jari alas tabung dan t adalah tinggi tabung. Rumus ini dapat digunakan untuk menghitung luas permukaan tabung dan menyelesaikan berbagai masalah praktis.
Pertanyaan 3: Mengapa luas selimut tabung penting dalam matematika, fisika, dan teknik?
Luas selimut tabung penting dalam matematika, fisika, dan teknik karena digunakan untuk menghitung volume tabung, gaya yang bekerja pada benda dalam fluida, dan luas permukaan pipa dan tangki. Memahami luas selimut tabung sangat penting untuk menyelesaikan berbagai masalah dalam bidang-bidang tersebut.
Pertanyaan 4: Apa saja contoh penerapan luas selimut tabung dalam bidang teknik?
Dalam bidang teknik, luas selimut tabung digunakan untuk menghitung luas permukaan pipa dan tangki. Luas permukaan pipa dan tangki diperlukan untuk menghitung jumlah bahan yang dibutuhkan untuk membuat pipa atau tangki tersebut. Memahami luas selimut tabung sangat penting untuk merancang dan membangun berbagai struktur dan sistem.
Kesimpulannya, luas selimut tabung merupakan konsep penting yang memiliki banyak aplikasi dalam kehidupan sehari-hari, matematika, fisika, dan teknik. Memahami luas selimut tabung sangat penting untuk menyelesaikan berbagai masalah praktis dan memperoleh wawasan yang lebih dalam tentang sifat dan perilaku tabung.
Artikel berikut akan memberikan tips tambahan untuk memahami luas selimut tabung secara lebih mendalam.
Tips Memahami Luas Selimut Tabung
Berikut adalah beberapa tips untuk memahami luas selimut tabung secara lebih mendalam:
Tip 1: Pahami Konsep Tabung
Sebelum mempelajari luas selimut tabung, penting untuk memahami konsep tabung terlebih dahulu. Tabung adalah bangun ruang tiga dimensi yang memiliki dua bidang lingkaran sejajar yang disebut alas dan tutup, serta selimut tabung yang menghubungkan alas dan tutup tersebut.
Tip 2: Hafalkan Rumus Luas Selimut Tabung
Rumus luas selimut tabung adalah L = 2r x t, di mana r adalah jari-jari alas tabung dan t adalah tinggi tabung. Hafalkan rumus ini dengan baik agar dapat digunakan untuk menyelesaikan masalah yang berkaitan dengan luas selimut tabung.
Tip 3: Latihan Soal
Cara terbaik untuk memahami luas selimut tabung adalah dengan latihan soal. Carilah soal-soal latihan yang berkaitan dengan luas selimut tabung dan cobalah untuk menyelesaikannya sendiri. Dengan latihan yang cukup, Anda akan semakin mahir dalam menghitung luas selimut tabung.
Tip 4: Terapkan dalam Kehidupan Nyata
Luas selimut tabung memiliki banyak aplikasi dalam kehidupan nyata, seperti menghitung luas permukaan kaleng minuman, pipa saluran air, dan tangki penyimpanan. Cobalah untuk menerapkan konsep luas selimut tabung dalam kehidupan sehari-hari untuk memahami konsep ini dengan lebih baik.
Dengan mengikuti tips-tips ini, Anda dapat memahami luas selimut tabung secara lebih mendalam dan menerapkannya untuk menyelesaikan masalah praktis yang melibatkan tabung.










