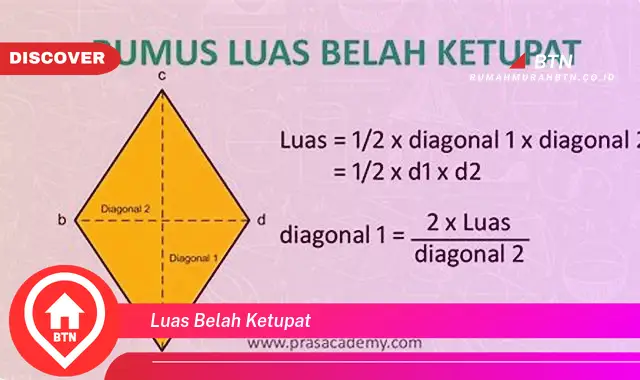
Luas belah ketupat adalah besaran yang menyatakan besarnya daerah yang ditempati oleh sebuah bangun datar belah ketupat. Belah ketupat merupakan bangun datar segi empat yang memiliki empat sisi sama panjang dan dua pasang sudut yang sama besar, yaitu sudut lancip dan sudut tumpul. Untuk menghitung luas belah ketupat, kita dapat menggunakan rumus:
Luas = (diagonal 1 x diagonal 2) / 2di mana diagonal 1 dan diagonal 2 adalah panjang diagonal-diagonal belah ketupat tersebut.
Mengetahui luas belah ketupat sangat penting dalam berbagai bidang, seperti arsitektur, teknik sipil, dan desain interior. Dengan mengetahui luas belah ketupat, kita dapat merencanakan dan membuat struktur atau objek yang memiliki bentuk belah ketupat dengan tepat. Selain itu, konsep luas belah ketupat juga memiliki sejarah panjang dalam matematika dan geometri, yang dapat ditelusuri kembali ke zaman Yunani kuno.
Dalam artikel ini, kita akan membahas lebih dalam tentang luas belah ketupat, termasuk cara menghitungnya, sifat-sifatnya, dan penerapannya dalam kehidupan sehari-hari. Kita juga akan membahas beberapa topik terkait, seperti keliling belah ketupat dan diagonal belah ketupat.
Luas Belah Ketupat
Luas belah ketupat merupakan besaran yang penting dalam matematika dan memiliki berbagai aplikasi dalam kehidupan sehari-hari. Berikut adalah empat aspek penting terkait luas belah ketupat:
-
Rumus: Luas belah ketupat dapat dihitung menggunakan rumus:
Luas = (diagonal 1 x diagonal 2) / 2, di mana diagonal 1 dan diagonal 2 adalah panjang diagonal-diagonal belah ketupat tersebut. - Sifat: Luas belah ketupat tidak berubah jika belah ketupat tersebut diputar atau dibalik.
- Penerapan: Luas belah ketupat digunakan dalam berbagai bidang, seperti arsitektur, teknik sipil, dan desain interior, untuk merencanakan dan membuat struktur atau objek yang memiliki bentuk belah ketupat.
- Sejarah: Konsep luas belah ketupat telah dikenal sejak zaman Yunani kuno, dan telah banyak digunakan dalam matematika dan geometri selama berabad-abad.
Keempat aspek ini saling terkait dan memberikan pemahaman yang komprehensif tentang luas belah ketupat. Rumus luas belah ketupat memungkinkan kita untuk menghitung luas belah ketupat dengan mudah dan akurat. Sifat-sifat luas belah ketupat membantu kita dalam menyelesaikan masalah geometri yang melibatkan belah ketupat. Penerapan luas belah ketupat menunjukkan pentingnya konsep ini dalam kehidupan nyata. Dan sejarah luas belah ketupat memberikan konteks tentang bagaimana konsep ini telah berkembang dan digunakan sepanjang waktu.
Rumus Luas Belah Ketupat
Rumus luas belah ketupat merupakan komponen penting dalam memahami konsep luas belah ketupat secara keseluruhan. Rumus ini memberikan metode yang sistematis dan akurat untuk menghitung luas belah ketupat, yang merupakan besaran penting dalam berbagai aplikasi praktis.
Dengan menggunakan rumus Luas = (diagonal 1 x diagonal 2) / 2, kita dapat menentukan luas belah ketupat berdasarkan panjang kedua diagonalnya. Diagonal adalah ruas garis yang menghubungkan dua titik sudut yang berlawanan pada belah ketupat. Dengan mengetahui panjang kedua diagonal, kita dapat menghitung luas belah ketupat dengan mudah dan cepat.
Pemahaman tentang rumus luas belah ketupat sangat penting dalam berbagai bidang, seperti arsitektur, teknik sipil, dan desain interior. Dalam arsitektur, rumus ini digunakan untuk menghitung luas lantai atau atap bangunan yang berbentuk belah ketupat. Dalam teknik sipil, rumus ini digunakan untuk menghitung luas jembatan atau jalan yang berbentuk belah ketupat. Dan dalam desain interior, rumus ini digunakan untuk menghitung luas karpet atau ubin lantai yang berbentuk belah ketupat.
Secara keseluruhan, rumus luas belah ketupat merupakan bagian integral dari pemahaman tentang luas belah ketupat. Rumus ini memberikan metode yang efektif untuk menghitung luas belah ketupat secara akurat, yang sangat penting dalam berbagai aplikasi praktis.
Sifat
Sifat ini merupakan salah satu sifat penting yang dimiliki oleh belah ketupat. Artinya, berapapun besar sudut yang dibentuk oleh diagonal-diagonal belah ketupat, luas belah ketupat tersebut akan tetap sama. Hal ini disebabkan oleh fakta bahwa ketika belah ketupat diputar atau dibalik, kedua diagonalnya akan tetap membentuk sudut siku-siku, sehingga panjang diagonal-diagonal tersebut tidak berubah. Akibatnya, luas belah ketupat yang dihitung menggunakan rumus Luas = (diagonal 1 x diagonal 2) / 2 juga akan tetap sama.
Sifat ini sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam arsitektur, ketika menghitung luas lantai atau atap bangunan yang berbentuk belah ketupat, kita tidak perlu khawatir dengan orientasi belah ketupat tersebut. Luas lantai atau atap akan tetap sama, berapapun besar sudut yang dibentuk oleh diagonal-diagonal belah ketupat. Demikian pula dalam teknik sipil, ketika menghitung luas jembatan atau jalan yang berbentuk belah ketupat, kita dapat menggunakan rumus luas belah ketupat tanpa perlu mempertimbangkan orientasi belah ketupat tersebut.
Pemahaman tentang sifat ini juga sangat penting dalam menyelesaikan masalah geometri yang melibatkan belah ketupat. Misalnya, kita dapat menggunakan sifat ini untuk membuktikan bahwa luas dua belah ketupat yang memiliki diagonal-diagonal yang sama adalah sama, meskipun bentuk dan orientasi kedua belah ketupat tersebut berbeda. Sifat ini juga dapat digunakan untuk menyelesaikan masalah yang melibatkan pembagian belah ketupat menjadi segitiga-segitiga yang lebih kecil.
Secara keseluruhan, sifat luas belah ketupat yang tidak berubah jika belah ketupat tersebut diputar atau dibalik merupakan sifat yang penting dan berguna dalam berbagai aplikasi praktis dan masalah geometri. Pemahaman tentang sifat ini memungkinkan kita untuk menyelesaikan masalah dan membuat perhitungan yang lebih efisien dan akurat.
Penerapan
Luas belah ketupat memiliki peran penting dalam berbagai aplikasi praktis di bidang arsitektur, teknik sipil, dan desain interior. Konsep luas belah ketupat digunakan untuk menghitung luas berbagai struktur dan objek yang berbentuk belah ketupat, sehingga dapat merencanakan dan membuat struktur atau objek tersebut dengan tepat dan efisien.
-
Arsitektur
Dalam arsitektur, luas belah ketupat digunakan untuk menghitung luas lantai atau atap bangunan yang berbentuk belah ketupat. Misalnya, ketika merancang sebuah rumah dengan atap berbentuk belah ketupat, arsitek perlu menghitung luas atap tersebut untuk menentukan kebutuhan bahan bangunan dan biaya konstruksi.
-
Teknik Sipil
Dalam teknik sipil, luas belah ketupat digunakan untuk menghitung luas jembatan atau jalan yang berbentuk belah ketupat. Misalnya, ketika merancang sebuah jembatan berbentuk belah ketupat, insinyur perlu menghitung luas jembatan tersebut untuk menentukan beban yang dapat ditopang oleh jembatan tersebut.
-
Desain Interior
Dalam desain interior, luas belah ketupat digunakan untuk menghitung luas karpet atau ubin lantai yang berbentuk belah ketupat. Misalnya, ketika mendesain sebuah ruangan dengan lantai berbentuk belah ketupat, desainer interior perlu menghitung luas lantai tersebut untuk menentukan jumlah karpet atau ubin lantai yang dibutuhkan.
Dengan memahami luas belah ketupat, para profesional di bidang arsitektur, teknik sipil, dan desain interior dapat merencanakan dan membuat struktur atau objek yang berbentuk belah ketupat dengan tepat dan efisien. Hal ini memastikan bahwa struktur atau objek tersebut memiliki bentuk dan ukuran yang sesuai dengan kebutuhan, sehingga dapat berfungsi dengan baik dan aman.
Sejarah
Konsep luas belah ketupat memiliki sejarah panjang yang berakar pada zaman Yunani kuno. Matematikawan Yunani seperti Pythagoras dan Euclid banyak berkontribusi pada pengembangan konsep ini. Mereka mengembangkan metode untuk menghitung luas belah ketupat dan membuktikan sifat-sifatnya, yang kemudian menjadi dasar bagi perkembangan matematika dan geometri selanjutnya.
Pemahaman tentang luas belah ketupat sangat penting dalam pengembangan arsitektur, teknik, dan seni pada zaman kuno. Arsitek Yunani menggunakan konsep ini untuk merancang bangunan dan kuil yang memiliki bentuk belah ketupat, seperti Parthenon di Athena. Insinyur Yunani menggunakan konsep ini untuk menghitung luas jembatan dan jalan yang berbentuk belah ketupat, seperti Jembatan Akropolis di Athena.
Selama berabad-abad, konsep luas belah ketupat terus berkembang dan digunakan dalam berbagai bidang, termasuk navigasi, astronomi, dan fisika. Penjelajah menggunakan konsep ini untuk menghitung luas pulau dan benua. Astronom menggunakan konsep ini untuk menghitung luas permukaan planet dan bintang. Fisikawan menggunakan konsep ini untuk menghitung luas permukaan benda dan untuk memahami sifat-sifat mekanika.
Pemahaman tentang sejarah luas belah ketupat sangat penting karena memberikan konteks tentang bagaimana konsep ini telah berkembang dan digunakan sepanjang waktu. Hal ini menunjukkan pentingnya konsep ini dalam matematika, geometri, dan berbagai bidang lainnya. Memahami sejarah luas belah ketupat juga memungkinkan kita untuk menghargai kontribusi para matematikawan dan ilmuwan masa lalu yang telah membentuk pemahaman kita tentang dunia.
Pertanyaan Umum tentang Luas Belah Ketupat
Bagian ini akan membahas beberapa pertanyaan umum tentang luas belah ketupat, meliputi definisi, rumus, sifat, dan penerapannya. Dengan memahami pertanyaan-pertanyaan umum ini, kita dapat memperoleh pemahaman yang lebih komprehensif tentang konsep luas belah ketupat.
Pertanyaan 1: Apa yang dimaksud dengan luas belah ketupat?
Luas belah ketupat adalah besaran yang menyatakan ukuran daerah yang ditempati oleh bangun datar belah ketupat. Belah ketupat merupakan bangun datar segi empat yang memiliki empat sisi sama panjang dan dua pasang sudut yang sama besar, yaitu sudut lancip dan sudut tumpul.
Pertanyaan 2: Bagaimana cara menghitung luas belah ketupat?
Luas belah ketupat dapat dihitung menggunakan rumus:
Luas = (diagonal 1 x diagonal 2) / 2di mana diagonal 1 dan diagonal 2 adalah panjang diagonal-diagonal belah ketupat tersebut.
Pertanyaan 3: Apa saja sifat-sifat luas belah ketupat?
Luas belah ketupat memiliki beberapa sifat, yaitu:
- Luas belah ketupat tidak berubah jika belah ketupat tersebut diputar atau dibalik.
- Luas belah ketupat sama dengan setengah luas persegi panjang yang memiliki panjang dan lebar sama dengan diagonal-diagonal belah ketupat tersebut.
Pertanyaan 4: Dalam bidang apa saja luas belah ketupat diterapkan?
Luas belah ketupat diterapkan dalam berbagai bidang, antara lain:
- Arsitektur: Menghitung luas lantai atau atap bangunan yang berbentuk belah ketupat.
- Teknik Sipil: Menghitung luas jembatan atau jalan yang berbentuk belah ketupat.
- Desain Interior: Menghitung luas karpet atau ubin lantai yang berbentuk belah ketupat.
Demikian beberapa pertanyaan umum tentang luas belah ketupat yang telah dibahas. Dengan memahami konsep-konsep ini, kita dapat lebih mudah dalam menyelesaikan masalah yang berkaitan dengan luas belah ketupat dalam kehidupan sehari-hari.
Untuk pemahaman yang lebih mendalam, silakan merujuk ke artikel tentang luas belah ketupat yang telah disediakan.
Tips Memahami Luas Belah Ketupat
Untuk memahami konsep luas belah ketupat dengan lebih baik, berikut adalah beberapa tips yang dapat diikuti:
Tip 1: Kuasai Rumus Luas Belah Ketupat
Rumus luas belah ketupat adalah dasar untuk menghitung luas belah ketupat. Pastikan untuk menghafal rumus Luas = (diagonal 1 x diagonal 2) / 2 dan memahami cara menggunakannya.
Tip 2: Pahami Sifat Luas Belah Ketupat
Luas belah ketupat memiliki sifat-sifat unik yang dapat membantu dalam menyelesaikan masalah. Pelajari dan pahami sifat-sifat tersebut, seperti sifat bahwa luas belah ketupat tidak berubah jika diputar atau dibalik.
Tip 3: Visualisasikan Belah Ketupat
Memvisualisasikan belah ketupat dapat membantu dalam memahami konsep luasnya. Bayangkan sebuah belah ketupat dan identifikasi diagonal-diagonalnya. Ini akan membuat perhitungan luas menjadi lebih mudah.
Tip 4: Praktikkan Soal-Soal
Cara terbaik untuk menguasai konsep luas belah ketupat adalah dengan berlatih soal-soal. Carilah soal-soal latihan dan cobalah selesaikan menggunakan rumus dan sifat-sifat luas belah ketupat. Dengan berlatih secara teratur, pemahaman akan semakin kuat.
Dengan mengikuti tips-tips ini, Anda dapat meningkatkan pemahaman tentang luas belah ketupat dan menyelesaikan masalah terkait dengan lebih mudah dan akurat.










