Intip Contoh Besaran Turunan yang Bikin Kamu Penasaran! – Jurnal BTN

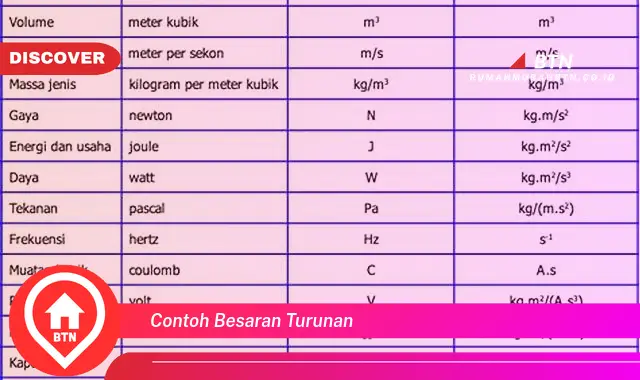
Besaran turunan merupakan besaran yang diturunkan dari besaran pokok melalui operasi matematika. Contoh besaran turunan antara lain: kecepatan, percepatan, gaya, usaha, dan energi.

Besaran turunan memiliki peran penting dalam berbagai bidang ilmu pengetahuan, seperti fisika, kimia, dan teknik. Besaran turunan membantu kita untuk mengukur dan menganalisis berbagai besaran yang ada di alam semesta. Selain itu, besaran turunan juga membantu kita untuk memahami hubungan antara besaran-besaran pokok dan besaran turunan.

Dalam artikel ini, kita akan membahas lebih lanjut tentang besaran turunan, termasuk jenis-jenis besaran turunan, satuan besaran turunan, dan penerapan besaran turunan dalam berbagai bidang ilmu pengetahuan.

Contoh Besaran Turunan

Besaran turunan merupakan besaran yang diturunkan dari besaran pokok melalui operasi matematika. Besaran turunan memiliki beberapa aspek penting, di antaranya:

• Jenis besaran turunan
• Satuan besaran turunan
• Penerapan besaran turunan
• Hubungan besaran turunan dengan besaran pokok

Jenis-jenis besaran turunan sangat beragam, di antaranya kecepatan, percepatan, gaya, usaha, dan energi. Setiap besaran turunan memiliki satuannya tersendiri, yang diturunkan dari satuan besaran pokok. Besaran turunan juga memiliki peran penting dalam berbagai bidang ilmu pengetahuan, seperti fisika, kimia, dan teknik.Dengan memahami konsep besaran turunan, kita dapat mengukur dan menganalisis berbagai besaran yang ada di alam semesta.

Jenis-Jenis Besaran Turunan

Besaran turunan memiliki jenis yang sangat beragam, di antaranya:

• Besaran skalar: Besaran skalar hanya memiliki besar, tanpa arah. Contoh besaran skalar antara lain massa, volume, dan suhu.
• Besaran vektor: Besaran vektor memiliki besar dan arah. Contoh besaran vektor antara lain kecepatan, percepatan, dan gaya.
• Besaran besaran pokok: Besaran pokok adalah besaran yang tidak dapat diturunkan dari besaran lain. Contoh besaran pokok antara lain panjang, massa, waktu, dan kuat arus listrik.
• Besaran besaran turunan: Besaran turunan adalah besaran yang diturunkan dari besaran pokok melalui operasi matematika. Contoh besaran turunan antara lain kecepatan, percepatan, dan gaya.

Jenis-jenis besaran turunan ini sangat penting untuk dipahami karena masing-masing jenis besaran turunan memiliki sifat dan penerapan yang berbeda-beda.

Satuan Besaran Turunan

Satuan besaran turunan merupakan satuan yang diturunkan dari satuan besaran pokok melalui operasi matematika. Satuan besaran turunan memiliki peran penting karena memungkinkan kita untuk mengukur dan menganalisis besaran turunan secara konsisten dan akurat.

• Jenis-Jenis Satuan Besaran Turunan

  Ada berbagai jenis satuan besaran turunan, antara lain satuan besaran skalar dan satuan besaran vektor. Satuan besaran skalar hanya memiliki besar, tanpa arah, sedangkan satuan besaran vektor memiliki besar dan arah.

• Penurunan Satuan Besaran Turunan

  Satuan besaran turunan diturunkan dari satuan besaran pokok melalui operasi matematika. Misalnya, satuan kecepatan (m/s) diturunkan dari satuan panjang (m) dan satuan waktu (s).

• Penerapan Satuan Besaran Turunan

  Satuan besaran turunan memiliki peran penting dalam berbagai bidang ilmu pengetahuan dan teknologi. Misalnya, satuan gaya (Newton) digunakan dalam fisika, satuan energi (Joule) digunakan dalam kimia, dan satuan daya (Watt) digunakan dalam teknik.

• Standarisasi Satuan Besaran Turunan

  Untuk memastikan konsistensi dan akurasi pengukuran, satuan besaran turunan telah distandarisasi secara internasional. Standarisasi ini dilakukan oleh organisasi seperti BIPM (Bureau International des Poids et Mesures).

Dengan memahami konsep satuan besaran turunan, kita dapat mengukur dan menganalisis besaran turunan secara lebih akurat dan konsisten. Hal ini sangat penting untuk kemajuan ilmu pengetahuan dan teknologi.

Penerapan Besaran Turunan dalam Kehidupan Sehari-hari

Besaran turunan memiliki peran penting dalam kehidupan sehari-hari. Berikut ini adalah beberapa penerapan besaran turunan dalam berbagai bidang:

• Dalam bidang fisika

  Besaran turunan seperti kecepatan, percepatan, gaya, dan energi digunakan dalam berbagai aplikasi fisika, seperti menghitung lintasan benda, menganalisis gaya yang bekerja pada benda, dan menentukan efisiensi mesin.

• Dalam bidang teknik

  Besaran turunan seperti gaya, tegangan, dan daya digunakan dalam berbagai aplikasi teknik, seperti merancang jembatan, menganalisis kekuatan bahan, dan menentukan efisiensi mesin.

• Dalam bidang kimia

  Besaran turunan seperti konsentrasi, pH, dan energi aktivasi digunakan dalam berbagai aplikasi kimia, seperti menentukan kecepatan reaksi, menganalisis kesetimbangan kimia, dan merancang proses kimia.

• Dalam bidang biologi

  Besaran turunan seperti kecepatan pertumbuhan, laju respirasi, dan konsentrasi hormon digunakan dalam berbagai aplikasi biologi, seperti menganalisis pertumbuhan populasi, menentukan metabolisme sel, dan mendiagnosis penyakit.

Dengan memahami konsep dan penerapan besaran turunan, kita dapat lebih memahami berbagai fenomena di alam semesta dan mengembangkan teknologi baru untuk meningkatkan kehidupan manusia.

Hubungan Besaran Turunan dengan Besaran Pokok

Besaran turunan memiliki hubungan yang erat dengan besaran pokok. Besaran turunan diturunkan dari besaran pokok melalui operasi matematika, sehingga sifat dan karakteristik besaran turunan dipengaruhi oleh besaran pokok yang digunakan untuk menurunkannya.

Sebagai contoh, besaran kecepatan adalah besaran turunan yang diturunkan dari besaran pokok panjang dan waktu. Kecepatan didefinisikan sebagai perubahan panjang terhadap perubahan waktu. Oleh karena itu, sifat dan karakteristik besaran kecepatan, seperti satuan (m/s) dan cara pengukurannya, dipengaruhi oleh sifat dan karakteristik besaran pokok panjang dan waktu.

Memahami hubungan antara besaran turunan dan besaran pokok sangat penting karena memungkinkan kita untuk menganalisis dan memahami berbagai fenomena alam secara lebih mendalam. Dengan memahami bagaimana besaran turunan diturunkan dari besaran pokok, kita dapat memperoleh pemahaman yang lebih baik tentang hubungan antara besaran-besaran tersebut dan bagaimana besaran-besaran tersebut dapat digunakan untuk memecahkan masalah dan mengembangkan teknologi baru.

Pertanyaan Umum tentang Besaran Turunan

Bagian ini menyajikan beberapa pertanyaan umum dan jawabannya mengenai besaran turunan. Pertanyaan-pertanyaan ini dipilih berdasarkan keseringan muncul dan kesalahpahaman umum yang terkait dengan topik ini.

Pertanyaan 1: Apa yang dimaksud dengan besaran turunan?

Besaran turunan adalah besaran yang diturunkan dari besaran pokok melalui operasi matematika. Besaran pokok adalah besaran yang berdiri sendiri dan tidak dapat diturunkan dari besaran lain, seperti panjang, massa, dan waktu. Sementara itu, besaran turunan diperoleh dari besaran pokok melalui operasi matematika, seperti perkalian, pembagian, atau kombinasi keduanya. Contoh besaran turunan antara lain kecepatan, percepatan, gaya, dan usaha.

Pertanyaan 2: Apa saja jenis-jenis besaran turunan?

Besaran turunan dapat diklasifikasikan menjadi dua jenis utama, yaitu besaran skalar dan besaran vektor. Besaran skalar hanya memiliki besar, sedangkan besaran vektor memiliki besar dan arah. Contoh besaran skalar adalah massa, volume, dan suhu. Contoh besaran vektor adalah kecepatan, percepatan, dan gaya.

Pertanyaan 3: Bagaimana cara menurunkan besaran turunan?

Besaran turunan diturunkan dari besaran pokok melalui operasi matematika. Operasi matematika yang digunakan tergantung pada definisi besaran turunan yang bersangkutan. Misalnya, kecepatan adalah besaran turunan yang didefinisikan sebagai perubahan jarak terhadap perubahan waktu. Oleh karena itu, kecepatan dapat diturunkan melalui operasi pembagian jarak dengan waktu.

Pertanyaan 4: Apa saja penerapan besaran turunan dalam kehidupan sehari-hari?

Besaran turunan memiliki banyak penerapan dalam kehidupan sehari-hari, terutama dalam bidang sains, teknik, dan teknologi. Misalnya, besaran kecepatan digunakan dalam navigasi dan transportasi, besaran gaya digunakan dalam konstruksi dan teknik mesin, serta besaran energi digunakan dalam produksi dan konsumsi energi.

Dengan memahami konsep besaran turunan dan penerapannya, kita dapat memperoleh pemahaman yang lebih baik tentang berbagai fenomena alam dan mengembangkan teknologi baru untuk meningkatkan kehidupan manusia.

Tips untuk Memahami Besaran Turunan

Berikut adalah beberapa tips untuk membantu Anda memahami besaran turunan:

• Pahami terlebih dahulu konsep besaran pokok dan besaran turunan.
• Pelajari definisi dan rumus untuk menurunkan berbagai besaran turunan.
• Terapkan besaran turunan pada soal-soal fisika, kimia, atau teknik untuk memperdalam pemahaman Anda.
• Diskusikan dengan teman atau guru jika Anda mengalami kesulitan memahami suatu konsep.

Dengan mengikuti tips-tips ini, Anda dapat meningkatkan pemahaman Anda tentang besaran turunan dan penerapannya dalam berbagai bidang.

Tips Memahami Besaran Turunan

Untuk memahami besaran turunan dengan lebih baik, berikut beberapa tips yang dapat diikuti:

Tip 1: Pahami Konsep Besaran Pokok dan Turunan
Langkah pertama dalam memahami besaran turunan adalah dengan memahami konsep besaran pokok dan turunan. Besaran pokok adalah besaran yang berdiri sendiri dan tidak dapat diturunkan dari besaran lain, seperti panjang, massa, dan waktu. Sementara itu, besaran turunan adalah besaran yang diturunkan dari besaran pokok melalui operasi matematika, seperti kecepatan, percepatan, dan gaya.

Tip 2: Pelajari Definisi dan Rumus
Setelah memahami konsep besaran pokok dan turunan, langkah selanjutnya adalah mempelajari definisi dan rumus untuk menurunkan berbagai besaran turunan. Definisi dan rumus ini dapat ditemukan dalam buku teks fisika atau sumber belajar lainnya. Dengan memahami definisi dan rumus, Anda dapat menurunkan besaran turunan yang dibutuhkan untuk memecahkan masalah atau menganalisis fenomena tertentu.

Tip 3: Terapkan dalam Soal Fisika
Untuk memperdalam pemahaman tentang besaran turunan, cobalah untuk menerapkannya pada soal-soal fisika. Latihan soal dapat membantu Anda memahami cara menggunakan besaran turunan dalam konteks yang sebenarnya. Mulailah dengan soal-soal sederhana dan secara bertahap tingkatkan tingkat kesulitan untuk menguji pemahaman Anda.

Tip 4: Diskusikan dengan Orang Lain
Jika Anda mengalami kesulitan memahami suatu konsep besaran turunan, jangan ragu untuk mendiskusikannya dengan teman, guru, atau ahli di bidang tersebut. Berdiskusi dengan orang lain dapat membantu Anda memperoleh perspektif yang berbeda dan memperjelas pemahaman Anda tentang topik tersebut.

Dengan mengikuti tips-tips ini, Anda dapat meningkatkan pemahaman Anda tentang besaran turunan dan penerapannya dalam berbagai bidang.