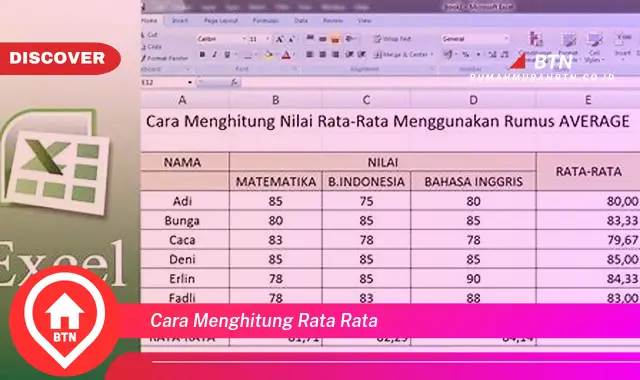
Rata-rata adalah ukuran yang banyak digunakan untuk mengukur nilai tengah suatu kumpulan data. Rata-rata dihitung dengan menjumlahkan semua nilai dalam kumpulan data dan kemudian membaginya dengan jumlah nilai. Rata-rata dapat digunakan untuk membandingkan kumpulan data yang berbeda atau untuk melacak perubahan dalam kumpulan data dari waktu ke waktu.
Rata-rata adalah ukuran yang penting karena dapat memberikan informasi tentang tren dan pola dalam kumpulan data. Rata-rata juga dapat digunakan untuk membuat prediksi tentang nilai masa depan dalam kumpulan data. Misalnya, rata-rata nilai ujian siswa dapat digunakan untuk memprediksi nilai ujian siswa di masa depan.
Rata-rata memiliki sejarah panjang dalam matematika dan statistik. Konsep rata-rata pertama kali diperkenalkan oleh matematikawan Yunani kuno Archimedes. Archimedes menggunakan rata-rata untuk menghitung luas dan volume berbagai bentuk. Sejak saat itu, rata-rata telah menjadi ukuran yang banyak digunakan dalam berbagai bidang, termasuk sains, bisnis, dan keuangan.
Cara Menghitung Rata-rata
Rata-rata merupakan ukuran penting yang digunakan untuk mengukur nilai tengah suatu kumpulan data. Menghitung rata-rata cukup mudah, namun pemahaman mendalam tentang konsep dan penerapannya sangat penting. Berikut adalah empat aspek penting dalam menghitung rata-rata:
- Jumlah: Menjumlahkan semua nilai dalam kumpulan data.
- Pembagian: Membagi jumlah dengan banyaknya nilai dalam kumpulan data.
- Nilai Tengah: Hasil pembagian, yang mewakili nilai tengah kumpulan data.
- Tren: Rata-rata dapat menunjukkan tren atau perubahan dalam kumpulan data.
Keempat aspek ini saling terkait dan membentuk proses menghitung rata-rata. Misalnya, jika kita memiliki kumpulan data nilai ujian siswa, kita dapat menghitung rata-rata dengan menjumlahkan semua nilai dan membaginya dengan jumlah siswa. Rata-rata ini akan memberikan gambaran tentang nilai tengah siswa secara keseluruhan. Selain itu, kita dapat membandingkan rata-rata nilai ujian dari waktu ke waktu untuk mengidentifikasi tren atau perubahan dalam kinerja siswa.
Jumlah
Jumlah merupakan langkah awal yang krusial dalam menghitung rata-rata. Tanpa menjumlahkan semua nilai dalam kumpulan data, kita tidak dapat memperoleh nilai total yang akan dibagi untuk mendapatkan rata-rata. Proses penjumlahan ini memastikan bahwa setiap nilai dalam kumpulan data diperhitungkan dan berkontribusi pada nilai rata-rata akhir.
Sebagai contoh, misalkan kita ingin menghitung rata-rata nilai ujian matematika dari 10 siswa. Pertama-tama, kita harus menjumlahkan semua nilai ujian, seperti 85, 92, 78, 90, 82, 88, 95, 80, 91, dan 86. Penjumlahan ini menghasilkan nilai total 887.
Dengan memahami pentingnya jumlah dalam menghitung rata-rata, kita dapat memperoleh representasi yang akurat dari nilai tengah suatu kumpulan data. Langkah ini menjadi dasar bagi langkah pembagian selanjutnya, yang akan menghasilkan nilai rata-rata yang bermakna.
Pembagian
Pembagian merupakan langkah penting dalam menghitung rata-rata. Setelah menjumlahkan semua nilai dalam kumpulan data, kita perlu membagi jumlah tersebut dengan banyaknya nilai dalam kumpulan data. Proses pembagian ini akan menghasilkan nilai rata-rata yang mewakili nilai tengah dari kumpulan data.
- Menghitung Banyaknya Nilai: Sebelum membagi jumlah, kita perlu menentukan banyaknya nilai dalam kumpulan data. Misalnya, jika kita memiliki kumpulan data nilai ujian matematika dari 10 siswa, maka banyaknya nilai dalam kumpulan data adalah 10.
- Melakukan Pembagian: Setelah memperoleh jumlah dan banyaknya nilai, kita dapat melakukan pembagian. Dalam contoh nilai ujian matematika, kita membagi jumlah nilai (887) dengan banyaknya nilai (10). Hasil pembagian tersebut adalah 88,7, yang merupakan nilai rata-rata nilai ujian matematika dari 10 siswa.
Dengan memahami pentingnya pembagian dalam menghitung rata-rata, kita dapat memperoleh representasi yang akurat dari nilai tengah suatu kumpulan data. Langkah ini melengkapi langkah penjumlahan sebelumnya, menghasilkan nilai rata-rata yang bermakna dan dapat digunakan untuk berbagai tujuan analisis data.
Nilai Tengah
Nilai tengah merupakan hasil pembagian jumlah nilai dengan banyaknya nilai dalam suatu kumpulan data. Nilai tengah ini merepresentasikan nilai rata-rata atau nilai yang berada di tengah-tengah distribusi data. Dalam konteks “cara menghitung rata rata”, nilai tengah menjadi tujuan utama yang ingin dicapai.
- Nilai Representatif: Nilai tengah berfungsi sebagai nilai representatif dari keseluruhan kumpulan data. Dengan mengetahui nilai tengah, kita dapat memperoleh gambaran umum tentang kecenderungan atau pola yang terdapat dalam data.
- Pembanding Kinerja: Nilai tengah dapat digunakan sebagai pembanding kinerja atau pencapaian. Misalnya, dalam dunia pendidikan, nilai tengah ujian dapat dijadikan patokan untuk menilai prestasi siswa secara keseluruhan.
- Dasar Pengambilan Keputusan: Nilai tengah dapat menjadi dasar dalam pengambilan keputusan. Misalnya, dalam dunia bisnis, nilai tengah penjualan dapat digunakan untuk memprediksi tren pasar atau merencanakan strategi pemasaran.
- Analisis Tren: Nilai tengah dapat digunakan untuk menganalisis tren atau perubahan dalam suatu kumpulan data. Dengan membandingkan nilai tengah dari waktu ke waktu, kita dapat mengidentifikasi pola atau kecenderungan yang terjadi.
Dengan memahami konsep nilai tengah dan perannya dalam “cara menghitung rata rata”, kita dapat memperoleh informasi yang berharga dari suatu kumpulan data. Nilai tengah menjadi ukuran statistik yang sangat penting dalam berbagai bidang, mulai dari akademisi hingga dunia bisnis.
Tren
Dalam “cara menghitung rata rata”, aspek tren memegang peranan penting. Rata-rata dapat memberikan gambaran tentang kecenderungan atau perubahan dalam suatu kumpulan data dari waktu ke waktu. Dengan membandingkan nilai rata-rata dari periode yang berbeda, kita dapat mengidentifikasi pola atau tren yang terjadi.
Kemampuan rata-rata dalam menunjukkan tren sangat bermanfaat dalam berbagai bidang. Misalnya, dalam dunia bisnis, rata-rata penjualan dapat digunakan untuk menganalisis tren pasar. Dengan mengamati perubahan rata-rata penjualan dari bulan ke bulan atau tahun ke tahun, perusahaan dapat mengidentifikasi pola musiman, pengaruh faktor eksternal, atau dampak strategi pemasaran.
Selain itu, rata-rata juga dapat digunakan untuk melacak kinerja atau pencapaian. Dalam dunia pendidikan, misalnya, rata-rata nilai ujian dapat digunakan untuk menganalisis tren prestasi siswa. Dengan membandingkan rata-rata nilai ujian dari semester ke semester atau tahun ke tahun, sekolah dapat mengidentifikasi bidang yang perlu ditingkatkan atau strategi pengajaran yang efektif.
Memahami hubungan antara rata-rata dan tren sangat penting dalam “cara menghitung rata rata”. Dengan menganalisis tren dalam suatu kumpulan data, kita dapat memperoleh wawasan yang berharga tentang pola, perubahan, dan faktor-faktor yang memengaruhinya. Hal ini memungkinkan kita untuk membuat prediksi yang lebih akurat, mengambil keputusan yang lebih tepat, dan mengoptimalkan strategi berdasarkan tren yang teridentifikasi.
Pertanyaan Umum tentang Cara Menghitung Rata-rata
Bagian ini menyediakan jawaban atas pertanyaan umum tentang cara menghitung rata-rata. Memahami konsep dan penerapan rata-rata sangat penting untuk memperoleh wawasan yang berharga dari data.
Pertanyaan 1: Apa saja langkah-langkah menghitung rata-rata?
Menghitung rata-rata melibatkan tiga langkah utama: menjumlahkan semua nilai dalam kumpulan data, membagi jumlah tersebut dengan banyaknya nilai, dan memperoleh nilai tengah yang mewakili rata-rata.
Pertanyaan 2: Mengapa rata-rata penting?
Rata-rata penting karena memberikan informasi tentang nilai tengah suatu kumpulan data. Rata-rata dapat digunakan untuk membandingkan kumpulan data yang berbeda, melacak perubahan dari waktu ke waktu, dan membuat prediksi tentang nilai masa depan.
Pertanyaan 3: Bagaimana cara menghitung rata-rata tertimbang?
Rata-rata tertimbang memperhitungkan kepentingan relatif dari nilai-nilai yang berbeda dalam kumpulan data. Untuk menghitung rata-rata tertimbang, kalikan setiap nilai dengan bobotnya, jumlahkan hasil perkalian tersebut, lalu bagi dengan jumlah bobot.
Pertanyaan 4: Apa saja kegunaan rata-rata dalam kehidupan nyata?
Rata-rata memiliki banyak kegunaan dalam kehidupan nyata, seperti menganalisis tren pasar, merencanakan strategi bisnis, mengevaluasi kinerja siswa, dan mengambil keputusan berdasarkan data.
Dengan memahami konsep dan penerapan rata-rata, kita dapat memperoleh manfaat maksimal dari data yang tersedia dan membuat keputusan yang lebih tepat.
Beralih ke bagian Tips akan memberikan panduan praktis untuk menghitung rata-rata secara efisien dan akurat.
Tips Menghitung Rata-rata
Tips berikut akan membantu Anda menghitung rata-rata secara efisien dan akurat:
Tip 1: Susun Data dengan Rapi
Susun data dalam urutan tertentu, seperti urutan menaik atau menurun. Pengurutan ini akan memudahkan proses penjumlahan dan pembagian.
Tip 2: Gunakan Kalkulator atau Spreadsheet
Gunakan kalkulator atau spreadsheet untuk mempercepat proses penjumlahan dan pembagian, terutama saat berhadapan dengan kumpulan data yang besar.
Tip 3: Periksa Ulang Hasil Perhitungan
Setelah menghitung rata-rata, periksa kembali hasil perhitungan Anda untuk memastikan tidak ada kesalahan penjumlahan atau pembagian.
Tip 4: Pertimbangkan Rata-rata Tertimbang
Dalam situasi tertentu, rata-rata tertimbang mungkin lebih sesuai. Rata-rata tertimbang memperhitungkan bobot atau kepentingan relatif dari setiap nilai dalam kumpulan data.
Dengan mengikuti tips ini, Anda dapat menghitung rata-rata secara lebih efisien dan akurat, memungkinkan Anda memperoleh wawasan yang berharga dari data Anda.










