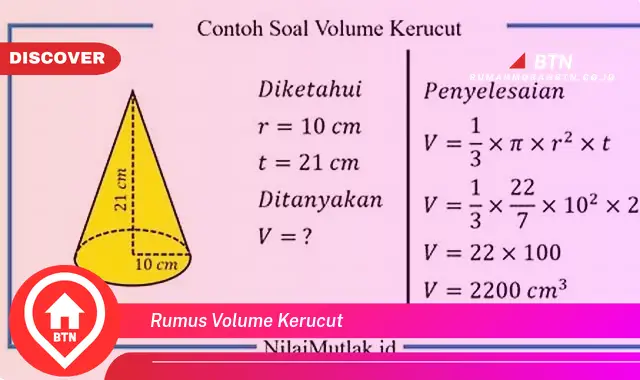
Rumus volume kerucut adalah sebuah persamaan matematika yang digunakan untuk menghitung volume suatu kerucut. Rumus ini dinyatakan sebagai:
V = (1/3)rt
di mana:
- V adalah volume kerucut
- adalah konstanta matematika yang nilainya sekitar 3,14
- r adalah jari-jari alas kerucut
- t adalah tinggi kerucut
Rumus volume kerucut sangat penting dalam banyak bidang, seperti teknik, arsitektur, dan desain. Rumus ini memungkinkan kita untuk menghitung volume berbagai objek berbentuk kerucut, seperti gelas, kerucut lalu lintas, dan bahkan gunung berapi.
Selain itu, rumus volume kerucut juga memiliki sejarah yang panjang dan menarik. Rumus ini pertama kali ditemukan oleh matematikawan Yunani Archimedes pada abad ke-3 SM. Archimedes menggunakan rumus ini untuk menghitung volume sebuah piramida, tetapi rumus yang sama juga dapat digunakan untuk menghitung volume kerucut.
Rumus volume kerucut adalah alat yang ampuh yang telah digunakan selama berabad-abad untuk menghitung volume berbagai objek berbentuk kerucut. Rumus ini merupakan bagian penting dari matematika dan memiliki banyak aplikasi dalam kehidupan nyata.
Rumus Volume Kerucut
Rumus volume kerucut merupakan persamaan matematika yang penting untuk menghitung volume bangun ruang berbentuk kerucut. Rumus ini memiliki beberapa aspek penting, yaitu:
- Volume: Rumus volume kerucut mengukur besarnya ruang yang ditempati oleh bangun ruang kerucut.
- Jari-jari: Jari-jari alas kerucut merupakan salah satu faktor yang menentukan volume kerucut.
- Tinggi: Tinggi kerucut juga merupakan faktor yang menentukan volume kerucut.
- Konstanta: Rumus volume kerucut menggunakan konstanta yang nilainya sekitar 3,14.
Keempat aspek ini saling terkait dan membentuk rumus volume kerucut, yaitu: V = (1/3)rt. Rumus ini dapat digunakan untuk menghitung volume berbagai macam benda berbentuk kerucut, seperti gelas, kerucut lalu lintas, dan bahkan gunung berapi. Dengan memahami aspek-aspek penting dari rumus volume kerucut, kita dapat menerapkan rumus ini secara efektif untuk menyelesaikan berbagai masalah matematika dan teknik.
Volume
Rumus volume kerucut berperan penting dalam menghitung volume bangun ruang berbentuk kerucut karena memungkinkan kita untuk menentukan besarnya ruang yang ditempati oleh kerucut tersebut. Volume suatu bangun ruang merupakan besaran yang sangat penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Dengan mengetahui volume suatu kerucut, kita dapat menghitung kapasitasnya, beratnya, dan sifat-sifat lainnya.
Sebagai contoh, dalam bidang teknik, rumus volume kerucut digunakan untuk menghitung volume tangki penyimpanan berbentuk kerucut. Dalam bidang arsitektur, rumus ini digunakan untuk menghitung volume ruang yang ditempati oleh atap berbentuk kerucut. Sementara dalam bidang desain, rumus ini digunakan untuk menghitung volume berbagai benda berbentuk kerucut, seperti vas bunga dan kap lampu.
Memahami hubungan antara rumus volume kerucut dan konsep volume sangat penting untuk dapat menerapkan rumus ini secara efektif dalam menyelesaikan masalah-masalah matematika dan teknik. Dengan memahami konsep volume dan bagaimana rumus volume kerucut digunakan untuk mengukurnya, kita dapat memperoleh wawasan yang lebih mendalam tentang sifat-sifat bangun ruang dan aplikasinya dalam kehidupan nyata.
Jari-jari
Hubungan antara jari-jari alas kerucut dan rumus volume kerucut sangatlah penting karena jari-jari alas merupakan salah satu faktor yang menentukan besarnya volume kerucut. Semakin besar jari-jari alas kerucut, maka semakin besar pula volumenya. Hal ini disebabkan karena jari-jari alas kerucut mempengaruhi luas alas kerucut, yang pada akhirnya mempengaruhi volume kerucut.
Dalam rumus volume kerucut, jari-jari alas kerucut diwakili oleh huruf “r”. Ketika jari-jari alas kerucut diperbesar, nilai “r” dalam rumus juga akan membesar. Akibatnya, nilai volume kerucut (V) juga akan membesar. Hal ini menunjukkan bahwa jari-jari alas kerucut memiliki pengaruh langsung terhadap volume kerucut.
Dalam aplikasi praktis, pemahaman hubungan antara jari-jari alas kerucut dan rumus volume kerucut sangat penting. Sebagai contoh, dalam bidang teknik, seorang insinyur perlu mempertimbangkan jari-jari alas kerucut ketika merancang tangki penyimpanan berbentuk kerucut. Dengan memperbesar jari-jari alas kerucut, insinyur dapat meningkatkan kapasitas penyimpanan tangki tanpa harus mengubah tinggi kerucut.
Contoh lain dapat ditemukan dalam bidang desain, di mana seorang desainer dapat menggunakan rumus volume kerucut untuk menentukan ukuran alas kerucut yang diperlukan untuk mencapai volume tertentu. Dengan memahami hubungan antara jari-jari alas kerucut dan volume kerucut, desainer dapat membuat benda berbentuk kerucut dengan ukuran yang sesuai dengan kebutuhan.
Kesimpulannya, jari-jari alas kerucut memiliki pengaruh yang signifikan terhadap volume kerucut. Dengan memahami hubungan ini dan menggunakan rumus volume kerucut, kita dapat menghitung volume kerucut secara akurat dan menerapkannya dalam berbagai bidang praktis, seperti teknik dan desain.
Tinggi
Kaitan antara tinggi kerucut dengan rumus volume kerucut sangat erat karena tinggi kerucut ikut menentukan besarnya volume kerucut. Semakin tinggi kerucut, maka semakin besar pula volumenya. Hal ini disebabkan karena tinggi kerucut mempengaruhi luas selimut kerucut, yang pada akhirnya mempengaruhi volume kerucut.
-
Pengaruh Tinggi Kerucut pada Volume
Dalam rumus volume kerucut, tinggi kerucut diwakili oleh huruf “t”. Ketika tinggi kerucut diperbesar, nilai “t” dalam rumus juga akan membesar. Akibatnya, nilai volume kerucut (V) juga akan membesar. Hal ini menunjukkan bahwa tinggi kerucut memiliki pengaruh langsung terhadap volume kerucut.
-
Aplikasi Praktis
Dalam aplikasi praktis, pemahaman hubungan antara tinggi kerucut dan rumus volume kerucut sangat penting. Misalnya, dalam bidang teknik, seorang insinyur perlu mempertimbangkan tinggi kerucut ketika merancang tangki penyimpanan berbentuk kerucut. Dengan memperbesar tinggi kerucut, insinyur dapat meningkatkan kapasitas penyimpanan tangki tanpa harus mengubah jari-jari alas kerucut.
-
Contoh Nyata
Contoh lain dapat ditemukan dalam bidang arsitektur, di mana seorang arsitek dapat menggunakan rumus volume kerucut untuk menentukan tinggi kerucut yang diperlukan untuk mencapai volume ruang tertentu. Dengan memahami hubungan antara tinggi kerucut dan volume kerucut, arsitek dapat membuat bangunan dengan atap berbentuk kerucut yang sesuai dengan kebutuhan.
-
Implikasi dalam Kehidupan Sehari-hari
Bahkan dalam kehidupan sehari-hari, hubungan antara tinggi kerucut dan volume kerucut dapat ditemui. Misalnya, saat membuat es krim berbentuk kerucut, semakin tinggi kerucut es krim, semakin banyak es krim yang dapat ditampung. Hal ini menunjukkan bahwa tinggi kerucut berperan penting dalam menentukan volume benda berbentuk kerucut.
Kesimpulannya, tinggi kerucut memiliki pengaruh yang signifikan terhadap volume kerucut. Dengan memahami hubungan ini dan menggunakan rumus volume kerucut, kita dapat menghitung volume kerucut secara akurat dan menerapkannya dalam berbagai bidang praktis, seperti teknik, arsitektur, dan bahkan dalam kehidupan sehari-hari.
Konstanta
Dalam rumus volume kerucut, terdapat sebuah konstanta matematika yang sangat penting, yaitu . Konstanta ini merupakan nilai tetap yang tidak berubah dan memiliki nilai sekitar 3,14. Kehadiran konstanta ini dalam rumus volume kerucut memiliki beberapa implikasi yang signifikan:
-
Menghitung Volume Secara Akurat
Konstanta memastikan bahwa rumus volume kerucut memberikan hasil yang akurat. Tanpa konstanta ini, rumus tersebut tidak akan dapat menghitung volume kerucut dengan benar. Konstanta ini mengoreksi perbedaan antara bentuk kerucut dan bentuk silinder, sehingga menghasilkan perhitungan volume yang tepat. -
Universalitas Rumus
Penggunaan konstanta membuat rumus volume kerucut menjadi universal. Rumus ini dapat digunakan untuk menghitung volume kerucut dengan berbagai ukuran dan bentuk, selama kerucut tersebut memiliki alas berbentuk lingkaran. Konstanta menjamin bahwa rumus tetap berlaku untuk semua kerucut, terlepas dari variasinya. -
Keterkaitan dengan Konsep Matematika Lain
Konstanta memiliki keterkaitan yang erat dengan konsep matematika lainnya, seperti keliling lingkaran dan luas lingkaran. Hal ini menunjukkan bahwa rumus volume kerucut tidak berdiri sendiri, tetapi merupakan bagian dari sistem matematika yang lebih besar. Pemahaman tentang keterkaitan ini dapat membantu dalam memecahkan masalah matematika yang lebih kompleks.
Kehadiran konstanta dalam rumus volume kerucut sangat penting karena memastikan akurasi, universalitas, dan keterkaitan dengan konsep matematika lainnya. Memahami peran konstanta ini sangat penting untuk menggunakan rumus volume kerucut secara efektif dan memperoleh hasil yang dapat diandalkan dalam berbagai aplikasi praktis.
Pertanyaan Umum tentang Rumus Volume Kerucut
Berikut adalah beberapa pertanyaan umum yang sering diajukan tentang rumus volume kerucut. Pertanyaan-pertanyaan ini akan dijawab dengan ringkas dan informatif.
Pertanyaan 1: Mengapa rumus volume kerucut menggunakan konstanta yang nilainya sekitar 3,14?
Jawaban: Konstanta digunakan untuk memastikan bahwa rumus volume kerucut memberikan hasil yang akurat. Selain itu, juga memberikan universalitas pada rumus, artinya rumus tersebut dapat digunakan untuk menghitung volume kerucut dengan berbagai ukuran dan bentuk.
Pertanyaan 2: Apa hubungan antara tinggi kerucut dan volumenya?
Jawaban: Tinggi kerucut memiliki pengaruh langsung terhadap volumenya. Semakin tinggi kerucut, semakin besar pula volumenya.
Pertanyaan 3: Bagaimana cara menggunakan rumus volume kerucut untuk menghitung volume kerucut terpancung?
Jawaban: Untuk menghitung volume kerucut terpancung, kita perlu mengetahui jari-jari alas atas, jari-jari alas bawah, dan tinggi kerucut terpancung. Rumus yang digunakan adalah: Volume = (1/3) (r1^2 + r2^2 + r1 r2) t, di mana r1 adalah jari-jari alas atas, r2 adalah jari-jari alas bawah, dan t adalah tinggi kerucut terpancung.
Pertanyaan 4: Dalam bidang apa saja rumus volume kerucut diterapkan?
Jawaban: Rumus volume kerucut memiliki banyak aplikasi di berbagai bidang, seperti teknik, arsitektur, dan desain. Dalam teknik, rumus ini digunakan untuk menghitung volume tangki penyimpanan berbentuk kerucut. Dalam arsitektur, rumus ini digunakan untuk menghitung volume ruang yang ditempati oleh atap berbentuk kerucut. Sementara itu, dalam desain, rumus ini digunakan untuk menghitung volume berbagai benda berbentuk kerucut, seperti vas bunga dan kap lampu.
Kesimpulan
Rumus volume kerucut adalah alat yang ampuh untuk menghitung volume berbagai benda berbentuk kerucut. Memahami konsep yang mendasari rumus ini dan cara menggunakannya secara efektif sangat penting untuk menyelesaikan masalah matematika dan teknik.
Tips Tambahan
Untuk mempelajari lebih lanjut tentang rumus volume kerucut, silakan baca artikel berikut: [Tautan ke Artikel Tips]
Tips Menguasai Rumus Volume Kerucut
Rumus volume kerucut sangat penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Berikut adalah beberapa tips untuk membantu Anda menguasai rumus ini:
Tip 1: Pahami Konsep Dasar
Sebelum mempelajari rumus volume kerucut, pastikan Anda memahami konsep dasar bangun ruang kerucut, seperti jari-jari alas, tinggi, dan garis pelukis. Memahami konsep-konsep ini akan memudahkan Anda memahami rumus dan penerapannya.
Tip 2: Hafalkan Rumusnya
Rumus volume kerucut adalah V = (1/3) r^2 * t. Hafalkan rumus ini dengan baik agar Anda dapat menggunakannya dengan mudah saat dibutuhkan. Anda juga dapat menuliskan rumus ini di tempat yang mudah terlihat, seperti di meja belajar atau dinding.
Tip 3: Latih Soal-Soal
Cara terbaik untuk menguasai rumus volume kerucut adalah dengan latihan soal. Carilah soal-soal latihan dari buku teks, internet, atau guru Anda. Dengan mengerjakan banyak soal, Anda akan semakin terbiasa menggunakan rumus dan meningkatkan pemahaman Anda.
Tip 4: Terapkan dalam Kehidupan Nyata
Untuk memperkuat pemahaman Anda tentang rumus volume kerucut, cobalah menerapkannya dalam kehidupan nyata. Misalnya, Anda dapat menghitung volume gelas berbentuk kerucut atau atap rumah berbentuk kerucut. Dengan menerapkan rumus dalam situasi nyata, Anda akan lebih memahami cara kerjanya dan manfaatnya.
Kesimpulan
Dengan mengikuti tips-tips di atas, Anda dapat menguasai rumus volume kerucut dengan baik. Rumus ini sangat berguna dalam berbagai bidang, jadi pastikan Anda memahaminya dengan benar agar dapat menyelesaikan masalah dan membuat keputusan yang tepat.










