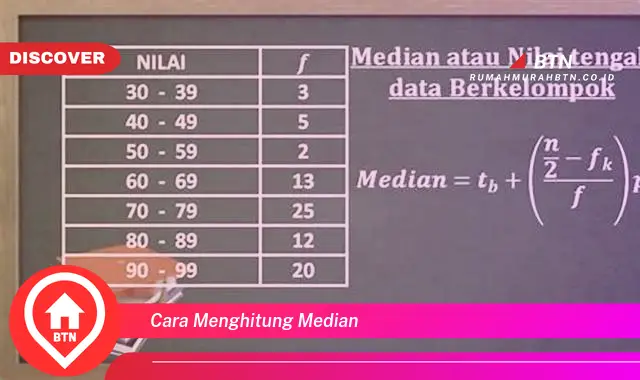
Median adalah nilai tengah dari suatu kumpulan data yang telah diurutkan dari yang terkecil hingga terbesar. Untuk menghitung median, terlebih dahulu urutkan data dari yang terkecil hingga terbesar, kemudian tentukan nilai tengahnya. Jika jumlah data ganjil, maka nilai tengah tersebut adalah mediannya. Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengah tersebut.
Median merupakan ukuran pemusatan yang banyak digunakan dalam statistika karena lebih tahan terhadap data ekstrem (outlier) dibandingkan dengan mean (rata-rata). Median juga mudah dihitung dan dipahami, sehingga banyak digunakan dalam berbagai bidang, seperti penelitian, bisnis, dan ekonomi.
Dalam artikel ini, kita akan membahas lebih lanjut tentang cara menghitung median, sifat-sifat median, dan penerapannya dalam berbagai bidang.
Cara Menghitung Median
Median merupakan ukuran pemusatan yang penting dalam statistika. Berikut adalah 4 aspek penting dalam memahami cara menghitung median:
- Mengurutkan Data: Data harus diurutkan dari yang terkecil hingga terbesar.
- Nilai Tengah: Untuk data ganjil, median adalah nilai tengah. Untuk data genap, median adalah rata-rata dari dua nilai tengah.
- Ketahanan Outlier: Median lebih tahan terhadap data ekstrem (outlier) dibandingkan mean.
- Aplikasi Luas: Median banyak digunakan dalam berbagai bidang, seperti penelitian, bisnis, dan ekonomi.
Memahami aspek-aspek ini penting untuk dapat menghitung median dengan benar. Sebagai contoh, jika kita memiliki data {2, 4, 6, 8, 10}, maka mediannya adalah 6. Jika kita memiliki data {2, 4, 6, 8, 10, 12}, maka mediannya adalah (8+10)/2 = 9. Median memberikan informasi yang valuable tentang kecenderungan sentral suatu kumpulan data, terutama ketika terdapat data ekstrem yang dapat mempengaruhi mean.
Mengurutkan Data
Mengurutkan data dari yang terkecil hingga terbesar merupakan langkah krusial dalam menghitung median. Tanpa mengurutkan data, kita tidak dapat menentukan nilai tengah, yang merupakan dasar perhitungan median. Proses pengurutan ini memungkinkan kita untuk mengidentifikasi urutan nilai data, sehingga kita dapat dengan mudah menemukan nilai tengah atau rata-rata dari dua nilai tengah.
Sebagai contoh, jika kita memiliki data {10, 2, 6, 8, 4}, kita harus mengurutkan data tersebut menjadi {2, 4, 6, 8, 10} sebelum menghitung median. Dengan mengurutkan data, kita dapat melihat bahwa nilai tengahnya adalah 6. Jika jumlah data genap, seperti pada data {10, 2, 6, 8}, kita akan mengurutkan data menjadi {2, 6, 8, 10} dan menghitung rata-rata dari dua nilai tengah, yaitu (6+8)/2 = 7. Jadi, median dari data tersebut adalah 7.
Memahami pentingnya mengurutkan data sebelum menghitung median sangat penting untuk memastikan akurasi dan keandalan hasil perhitungan. Dengan mengikuti langkah ini, kita dapat memperoleh informasi yang berharga tentang kecenderungan sentral suatu kumpulan data, yang sangat berguna dalam berbagai bidang seperti penelitian, bisnis, dan ekonomi.
Nilai Tengah
Menentukan nilai tengah merupakan langkah krusial dalam menghitung median. Dalam konteks “cara menghitung median”, nilai tengah memiliki peran penting dalam menentukan posisi data yang menjadi acuan median.
-
Nilai Tengah untuk Data Ganjil
Pada data ganjil, nilai tengah merupakan nilai yang berada di tengah-tengah kumpulan data setelah diurutkan. Sebagai contoh, pada data {3, 5, 7, 9}, nilai tengahnya adalah 7.
-
Nilai Tengah untuk Data Genap
Pada data genap, tidak terdapat satu nilai tengah yang jelas. Oleh karena itu, median dihitung sebagai rata-rata dari dua nilai tengah. Misalnya, pada data {3, 5, 7, 9, 11}, dua nilai tengahnya adalah 5 dan 7, sehingga mediannya adalah (5 + 7) / 2 = 6.
Dengan memahami konsep nilai tengah, kita dapat menghitung median secara akurat dan memperoleh informasi yang berharga tentang kecenderungan sentral suatu kumpulan data. Hal ini sangat penting dalam berbagai bidang, seperti penelitian, bisnis, dan ekonomi.
Ketahanan Outlier
Salah satu sifat penting dari median adalah ketahanannya terhadap outlier, atau data ekstrem yang jauh dari nilai-nilai lainnya dalam suatu kumpulan data. Berbeda dengan mean (rata-rata), yang dapat sangat terpengaruh oleh outlier, median tetap stabil dan memberikan representasi yang lebih akurat dari kecenderungan sentral data.
-
Pengaruh Outlier pada Mean
Mean sangat sensitif terhadap outlier. Jika ada satu atau beberapa nilai yang sangat besar atau sangat kecil dalam suatu kumpulan data, mean akan tertarik ke arah nilai-nilai tersebut. Hal ini dapat memberikan kesan yang menyesatkan tentang kecenderungan sentral data.
-
Median Tidak Terpengaruh Outlier
Median, di sisi lain, tidak terpengaruh oleh outlier. Nilai-nilai ekstrem tidak akan mengubah posisi nilai tengah atau rata-rata dari dua nilai tengah. Hal ini membuat median menjadi ukuran yang lebih andal untuk mewakili kecenderungan sentral data, terutama ketika terdapat outlier.
Ketahanan median terhadap outlier sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam penelitian medis, median sering digunakan untuk menganalisis data karena dapat memberikan gambaran yang lebih akurat tentang kecenderungan sentral ketika terdapat nilai-nilai ekstrem, seperti hasil tes yang sangat tinggi atau sangat rendah.
Aplikasi Luas
Berkat sifat-sifatnya yang unggul, median banyak digunakan dalam berbagai bidang untuk memberikan informasi berharga tentang kumpulan data. Beberapa bidang penerapan median antara lain:
- Penelitian: Dalam penelitian ilmiah, median digunakan untuk menganalisis data yang mungkin mengandung outlier atau nilai ekstrem. Median memberikan representasi kecenderungan sentral yang lebih akurat dibandingkan mean, terutama ketika terdapat data yang menyimpang.
- Bisnis: Dalam dunia bisnis, median digunakan untuk mengukur kinerja keuangan, seperti laba median dan pendapatan median. Ukuran-ukuran ini memberikan gambaran yang lebih jelas tentang tren bisnis daripada mean, yang dapat terdistorsi oleh nilai-nilai ekstrem.
- Ekonomi: Dalam ekonomi, median digunakan untuk menganalisis data pendapatan, pengeluaran, dan variabel ekonomi lainnya. Median memberikan ukuran yang lebih stabil dan representatif dari distribusi data dibandingkan mean, yang dapat dipengaruhi oleh kesenjangan pendapatan yang besar.
Penerapan median yang luas ini menunjukkan pentingnya memahami cara menghitung median dan menginterpretasikan hasilnya secara akurat. Dengan menguasai konsep-konsep dasar ini, kita dapat menggunakan median secara efektif untuk mendapatkan wawasan berharga dari kumpulan data di berbagai bidang.
Pertanyaan Umum tentang Cara Menghitung Median
Bagian ini berisi pertanyaan umum dan jawabannya mengenai cara menghitung median. Memahami pertanyaan-pertanyaan ini akan membantu Anda menguasai konsep median dan menerapkannya dengan tepat.
Pertanyaan 1: Apa perbedaan utama antara median dan mean?
Jawaban: Median adalah nilai tengah dari suatu kumpulan data yang telah diurutkan, sedangkan mean adalah rata-rata dari seluruh nilai data. Median lebih tahan terhadap data ekstrem (outlier) dibandingkan mean.
Pertanyaan 2: Mengapa penting untuk mengurutkan data sebelum menghitung median?
Jawaban: Mengurutkan data sangat penting karena median dihitung berdasarkan posisi nilai data setelah diurutkan. Tanpa mengurutkan data, Anda tidak dapat menentukan nilai tengah atau rata-rata dari dua nilai tengah.
Pertanyaan 3: Bagaimana cara menghitung median untuk data genap?
Jawaban: Untuk data genap, median dihitung sebagai rata-rata dari dua nilai tengah setelah data diurutkan.
Pertanyaan 4: Di bidang apa saja median banyak digunakan?
Jawaban: Median banyak digunakan dalam penelitian, bisnis, dan ekonomi untuk memberikan informasi yang berharga tentang kecenderungan sentral suatu kumpulan data, terutama ketika terdapat data ekstrem.
Memahami pertanyaan-pertanyaan umum ini akan membantu Anda menguasai konsep median dan menerapkannya dengan tepat dalam berbagai situasi.
Selanjutnya, artikel ini akan memberikan beberapa tips untuk menghitung median secara akurat dan efisien.
Tips Menghitung Median
Bagian ini menyajikan beberapa tips untuk membantu Anda menghitung median secara akurat dan efisien.
Tips 1: Buat Tabel atau Grafik
Membuat tabel atau grafik dari data Anda dapat memudahkan untuk mengurutkan data dan mengidentifikasi nilai tengah atau rata-rata dari dua nilai tengah.
Tips 2: Periksa Jumlah Data
Sebelum menghitung median, periksa apakah jumlah data ganjil atau genap. Hal ini akan menentukan apakah Anda akan langsung mengambil nilai tengah atau menghitung rata-rata dari dua nilai tengah.
Tips 3: Gunakan Kalkulator
Jika Anda memiliki kumpulan data yang besar, menggunakan kalkulator dapat mempercepat proses pengurutan dan penghitungan median.
Tips 4: Perhatikan Outlier
Jika terdapat outlier atau data ekstrem dalam kumpulan data Anda, pertimbangkan untuk menggunakan metode alternatif seperti trimmed mean atau median absolut deviasi untuk mendapatkan representasi kecenderungan sentral yang lebih akurat.
Dengan mengikuti tips ini, Anda dapat menghitung median dengan percaya diri dan memperoleh wawasan berharga dari kumpulan data Anda.










